- 1.树的基本概念和术语的问题
- 2.由二叉树的先序和中序序列建树
- 3.哈夫曼树和哈夫曼编码
- 4.图的基本概念
- 5.画出无向图的邻接表并写出图的广度和深度优先遍历序列
- 6.求最小生成树
- 7.求单源点的最短路径
- 10.顺序查找
- 11.二分查找或折半查找
- 12.二叉排序树
- 13.散列表查找——线性探测法
- 14.哈希表查找——链地址法
- 15.各种排序
[TOC]
1.树的基本概念和术语的问题
设在树中,结点x是结点y的双亲时,用(x,y)来表示树变。已知一棵树边的集合为:{(i,m),(i,n),(b,e),(e,i),(b,d),(a,b),(g,j),(g,k),(c,g),(c,f),(h,l),(c,h),(a,c)},回答下列问题:
(1)用树形表示法(带字母的圆圈和线)画出此树
(2) 哪个是根结点
(3) 哪些是叶结点?
(4) 哪个是g的双亲?
(5) 哪些是g的祖先?
(6) 哪些是g的孩子?
(7) 哪些是e的子孙?
(8) 哪些是e的兄弟?哪些是f的兄弟?
(9) 结点b和n的层次各是多少?
(10) 树的深度是多少?
(11) 以结点c为根的子树的深度是多少?
(12) 树的度数是多少?
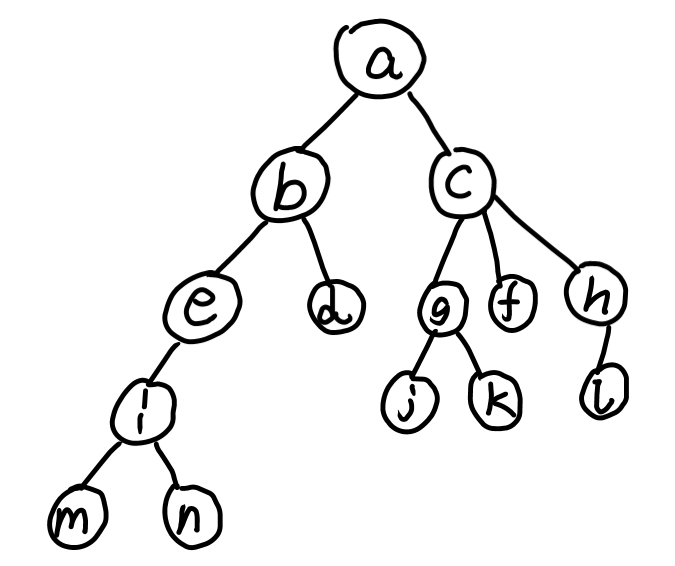
a是根结点;
m、n、d、j、k、f、l是叶子结点;
c是g的双亲;
a是g的祖先;
j、k是g的孩子;
i、m、n是e的子孙;
d是e的兄弟,g、h是f的兄弟;
b的层次是2,n的层次是5;
树的深度是5;
c的深度是3;
树的度数是3。
2.由二叉树的先序和中序序列建树

假设一棵二叉树的先序序列为EBADCFHGIKJ和中序序列为ABCDEFGHIJK,要求:
(1)画出这棵二叉树;
(2)请给出其后序序列和层序序列。

后序:ACDBGJKIHFE
层序:EBFADHCGIKJ
3.哈夫曼树和哈夫曼编码
求哈夫曼树:
(1)根据n个给定的权值构成n棵二叉树的森林,森林中每一棵树只有一个带权的根结点
(2)在森林中,选取两棵根结点的权值最小的树作为左右子树,构造一棵新的二叉树,且设置新的二叉树的根结点的权值为其左右子树上根结点的权值之和
(3)在森林中删除这两棵树,同时将新得到的二叉树加入到森林中
(4)重复(2)和(3),直到森林中只有一棵树为止,这棵树即为哈夫曼树
求哈夫曼编码:
左分支为0,右分支为1。
假设用于通信的电文仅由8个字母组成,字母在电文中出现的频率分别为0.09,0.16,0.02,0.06,0.32,0.03,0.21,0.11。
(1)画出哈夫曼树;
(2)根据哈夫曼树给这8个字母设计哈夫曼编码,计算WPL值;
(3)设计另一种由二进制表示的等长编码方案;
(4) 对于上述实例,计算两种方案的平均编码长度,分析两种方案的优缺点。
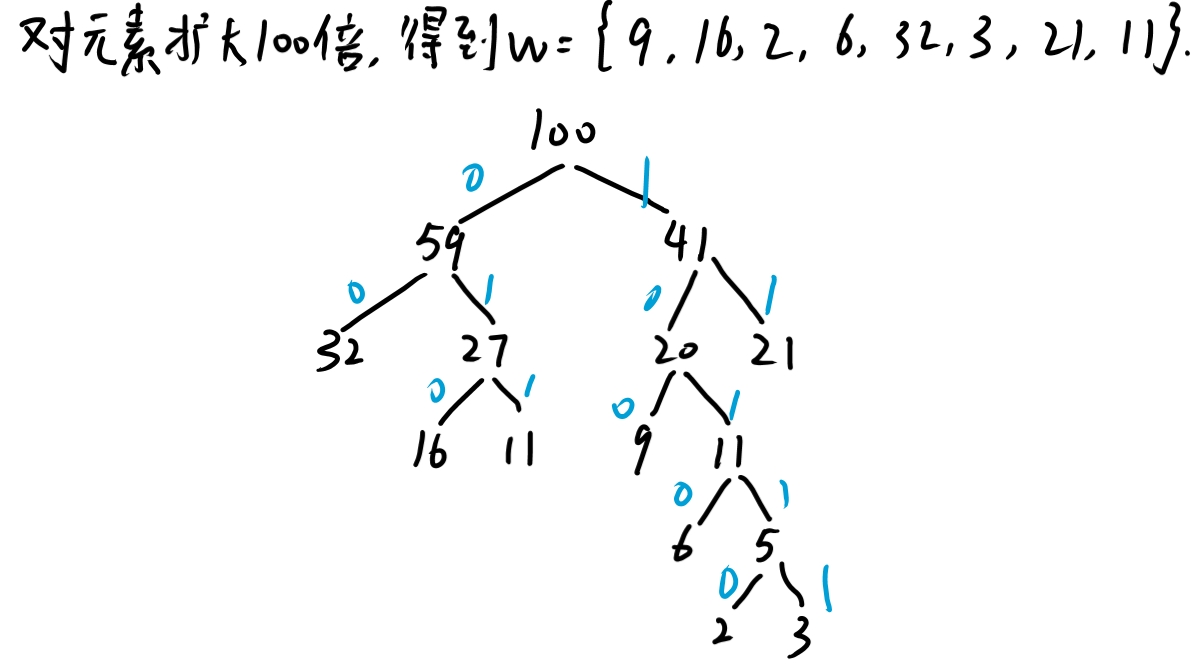
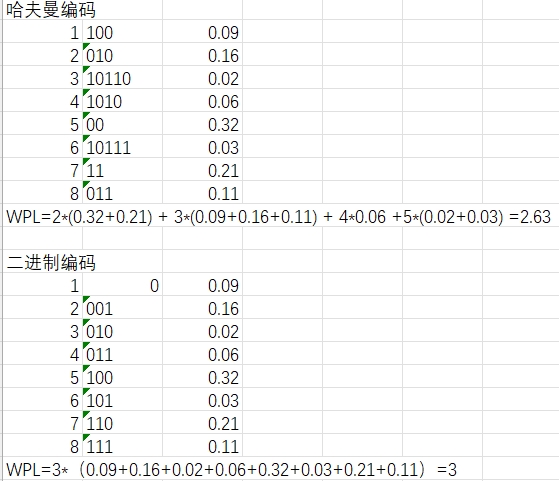
对于上述两种方案,等长编码的构造比哈夫曼编码的构造简单。等长编码的译码简单。但是哈夫曼编码是最优前缀编码。利用哈夫曼编码对文件进行编码,使该文件压缩后对应的二进制文件的长度最短。而等长编码使该二进制文件的长度不短。哈夫曼编码的构造和译码相对等长编码复杂些。
4.图的基本概念
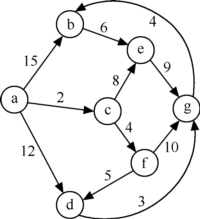
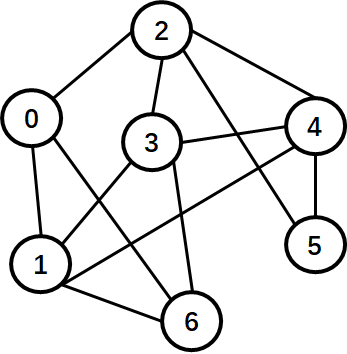
请根据下图给出:
(1)每个顶点的度
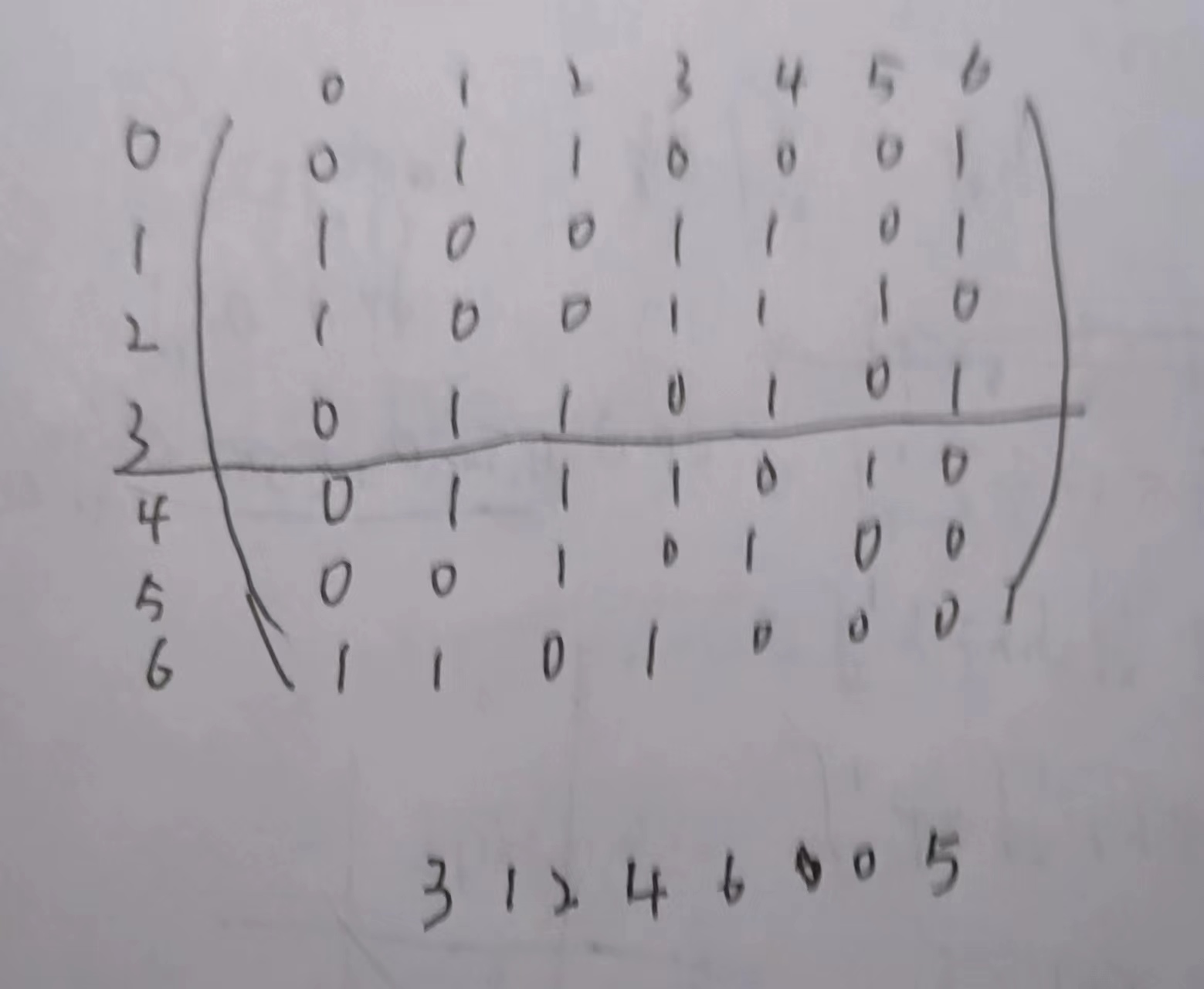
(2)邻接矩阵
(3)邻接表(边结点序号从小到大)

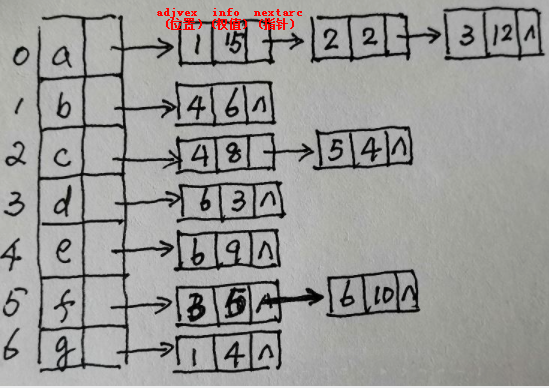
5.画出无向图的邻接表并写出图的广度和深度优先遍历序列
(1)写出下图的邻接表(边结点序号从小到大),
(2)写出从顶点3出发的广度优先搜索序列和深度优先搜索序列,顶点之间用空格隔开。约定以结点小编号优先次序访问。

广度:3 1 2 4 6 0 5
深度:3 1 0 2 4 5 6
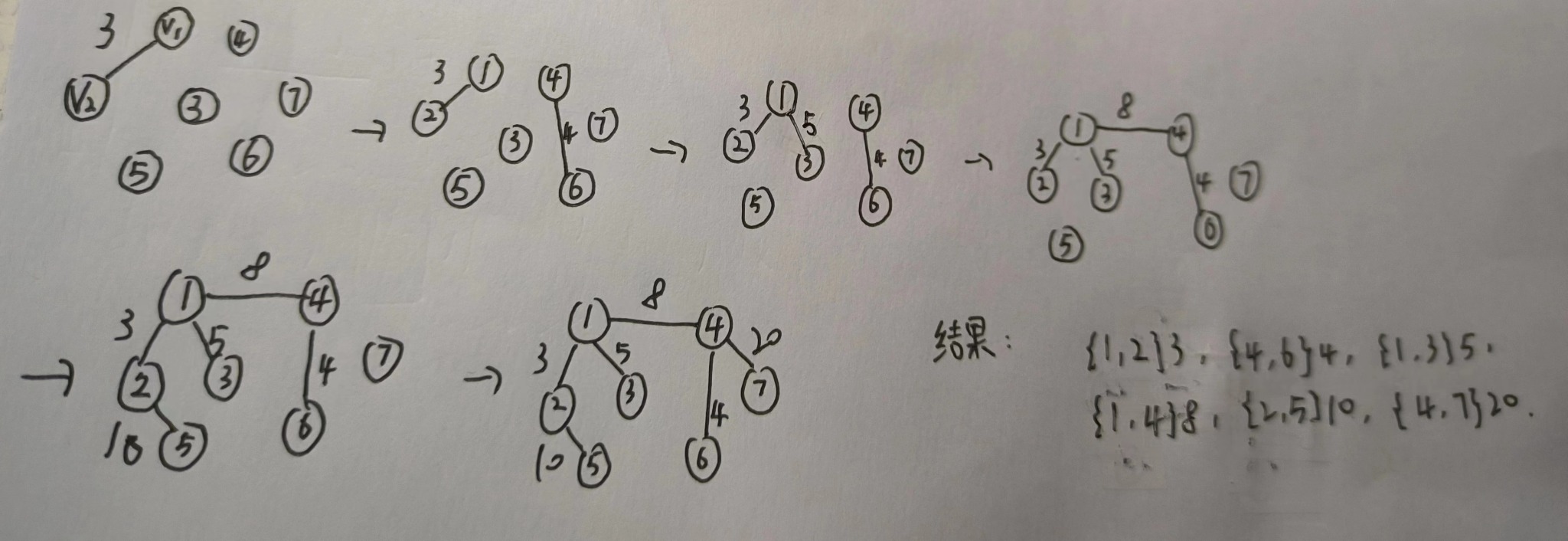
6.求最小生成树
已知一个无向图的顶点集V和边集E分别为:V={1,2,3,4,5,6,7};
E={(1,2)3, (1,3)5, (1,4)8, (2,5)10, (2,3)6, (3,4)15, (3,5)12, (3,6)9, (4,6)4, (4,7)20, (5,6)18, (6,7)25}; //每条边后面的数代表权值
请用克鲁斯卡尔算法得到最小生成树,试写出在最小生成树中依次得到的各条边。
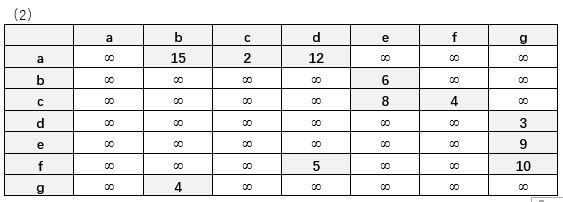
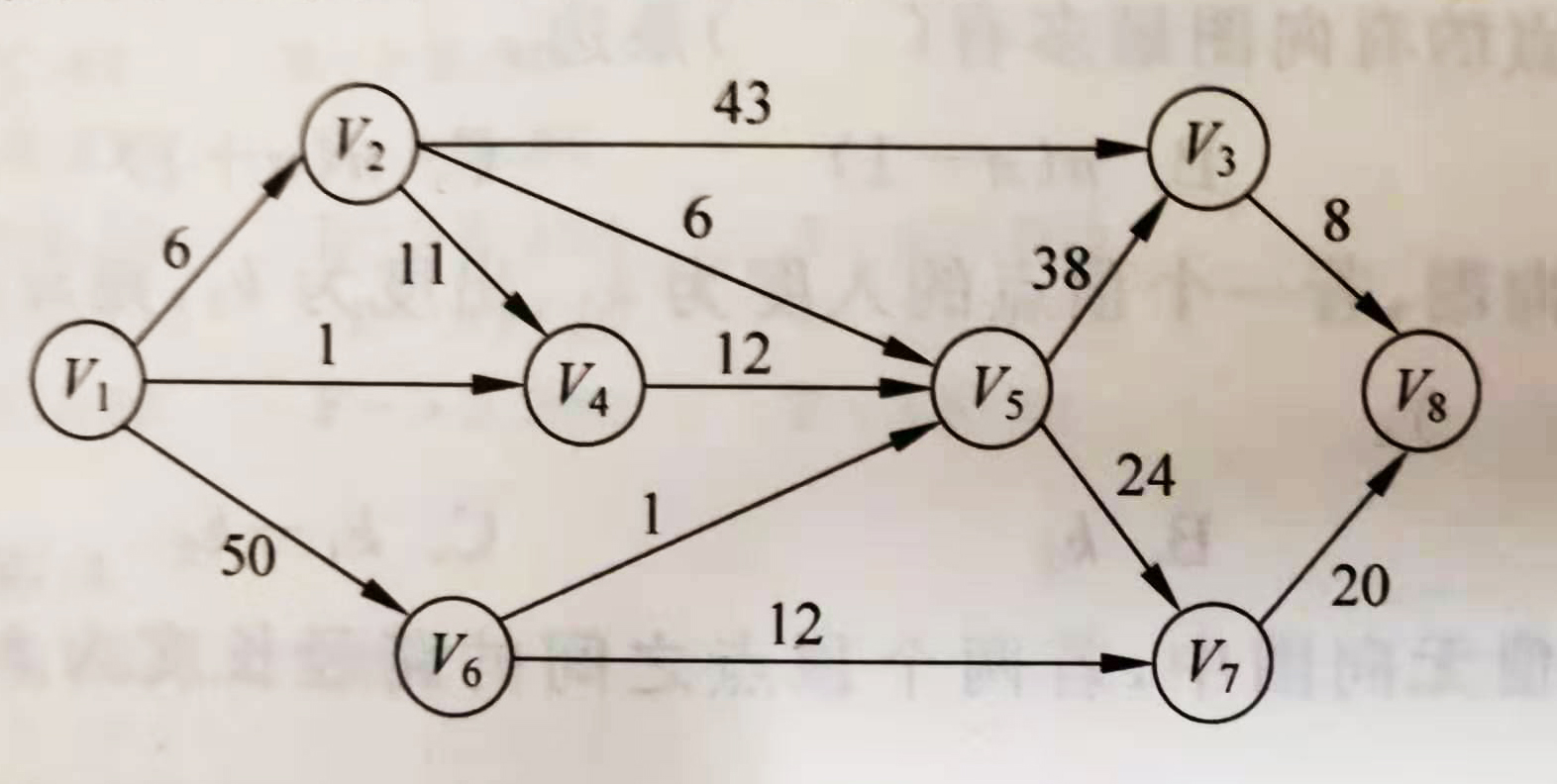
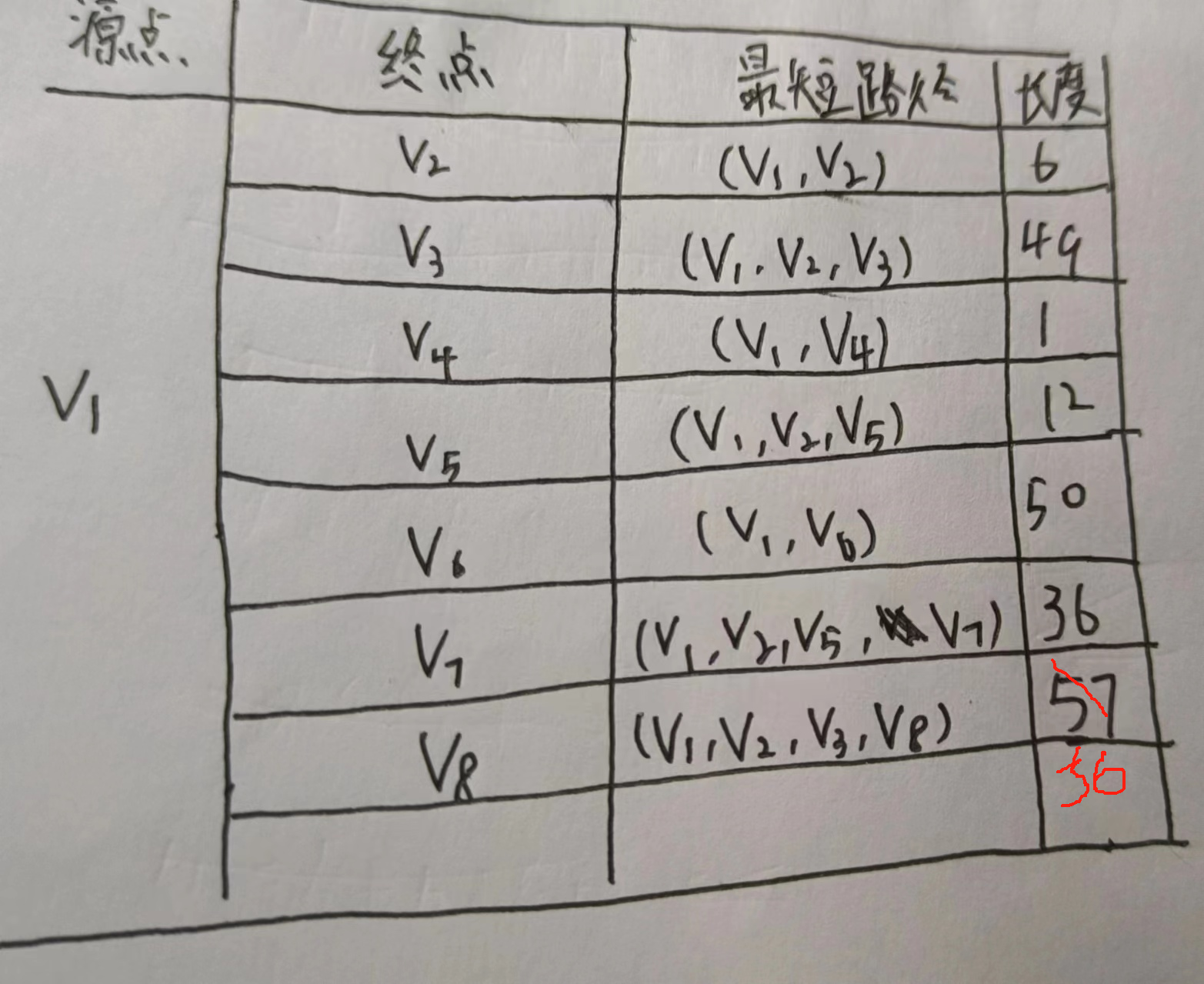
7.求单源点的最短路径
下图所示的带权有向图G,给出从顶点V1到其余各个顶点的最短路径及其路径长度。
10.顺序查找
根据教材中设置监视哨的顺序查找算法,回答如下问题:
(1)简述设置监视哨的顺序查找算法中监视哨的作用,(2)查找表中哪个数据元素是哨兵?(3)查找方向是顺序方向查找还是逆序方向查找?(4)n个元素的查找表进行设置监视哨的顺序查找,需要进行多少次比较后查找失败?
答案:
(1)设置监视哨,可以免去查找过程中每一步都要检测整个表是否查找完毕,可以使进行一次查找所需的平均时间几乎减少一半,提高了查找效率。
(2)顺序表ST的0单元
(3)逆序
(4)n+1次
11.二分查找或折半查找
已知如下11个元素的有序表(8,16,19,23,39,52,63,77,81,88,90),要求:
(1)画出其二分查找的判定树;
(2)给出查找元素88和17的折半查找过程;
(3)设有序表表长为n,查找成功或不成功时和给定值进行比较的关键字个数至多分别为多少?
(4)给出二分查找的时间复杂度。
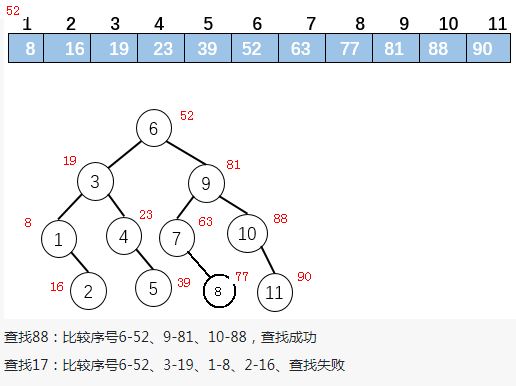

(3)查找成功和给定值进行比较的关键字个数至多都是(log₂n)的向下取整再加一
查找不成功和给定值进行比较的关键字个数等于该路径上内部结点个数,至多不超过(log₂n)的向下取整再加一
(4)O(log₂n)
12.二叉排序树
在一个空的二叉排序树中依次插入关键字序列为12,7,17,11,16,2,13,9,21,4,要求:
(1)画出所得到的二叉排序树;
(2)查找关键字9和22各自跟哪些关键字进行了比较?
(3)二叉排序树的平均查找长度(ASL)与其形态有关,对n个元素构建的二叉排序树进行查找,最好和最坏的ASL分别是多少?
保证左子树小于根节点,右子树大于根节点
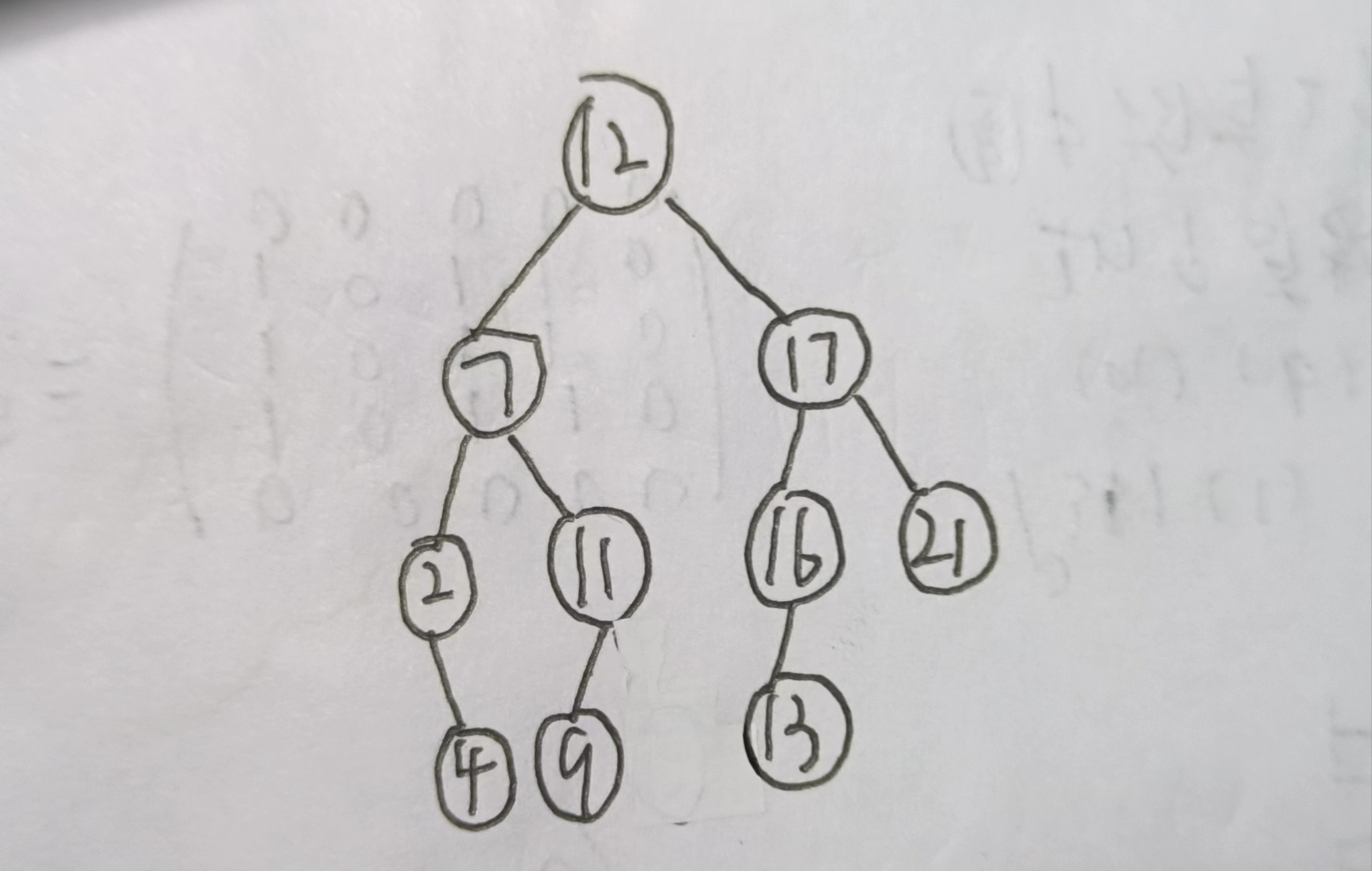
(2)9:12、7、11、9
22:12、17、21
(3)最好:log₂n
最坏:(n+1)/2
13.散列表查找——线性探测法
设哈希表的地址范围为0~17,哈希函数为:H(key)=key%16。用线性探测法处理冲突,输入关键字序列:(10,24,32,17,31,30,46,47,40,63,49),构造哈希表,试回答下列问题:
① 画出哈希表的示意图;
② 若查找关键字63,需要依次与哪些关键字进行比较?
③ 若查找关键字60,需要依次与哪些关键字比较?
④ 假定每个关键字的查找概率相等,求查找成功时的平均查找长度。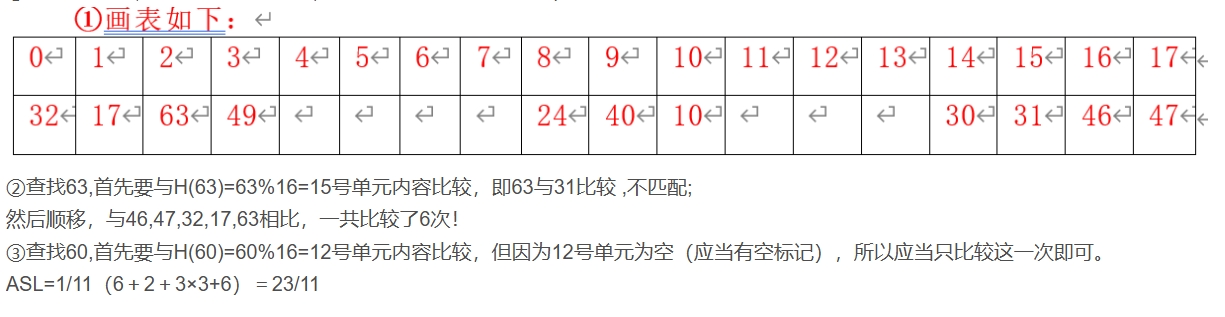
14.哈希表查找——链地址法
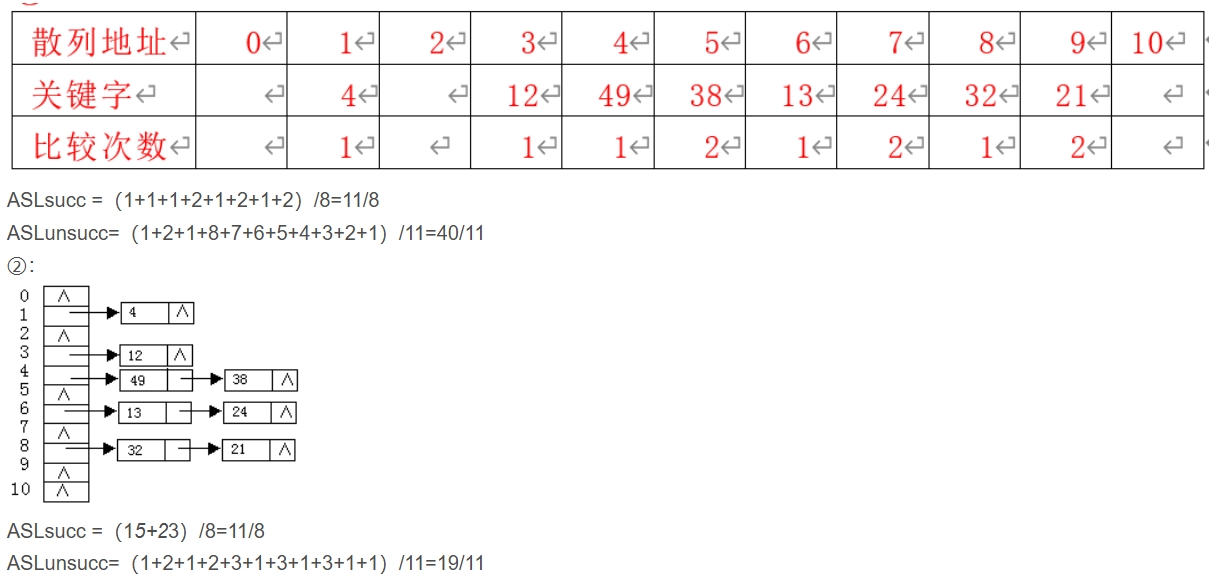
15.各种排序
(1)设待排序的关键字序列为{12,2,16,30,28,10,16*,20,6,18},试分别写出使用以下排序方法,每趟排序结束后关键字序列的状态。
① 直接插入排序
④ 冒泡排序
⑤ 快速排序
⑥ 简单选择排序
⑦ 堆排序
⑧ 二路归并排序
①直接插入排序

④ 冒泡排序

⑤ 快速排序
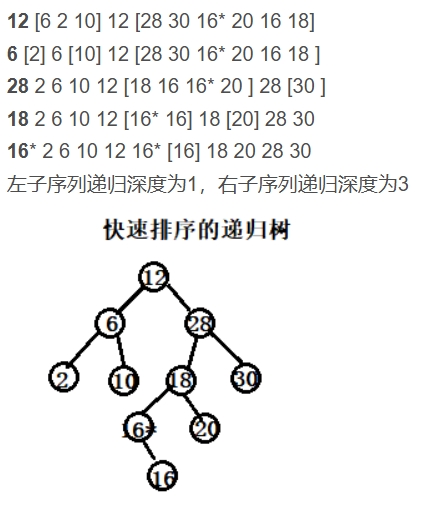
⑥ 简单选择排序
将最小的选出来放在前面
2 [12 16 30 28 10 16* 20 6 18]
2 6 [16 30 28 10 16* 20 12 18]
2 6 10 [30 28 16 16* 20 12 18]
2 6 10 12 [28 16 16* 20 30 18]
2 6 10 12 16 [28 16* 20 30 18]
2 6 10 12 16 16* [28 20 30 18]
2 6 10 12 16 16* 18 [20 30 28]
2 6 10 12 16 16* 18 20 [28 30]
2 6 10 12 16 16* 18 20 28 [30]
⑧ 二路归并排序
[2 12] [16 30] [10 28] [16 * 20] [6 18]
[2 12 16 30] [10 16* 20 28] [ 6 18 ]
[2 10 12 16 16* 20 28 30] [6 18]
2 6 10 12 16 16* 18 20 28 30