[TOC]

一、图的基本操作

int LocateVex();

// 返回顶点u在图中的位置

1
2
3
4
5
int LocateVex(MGraph G, VertexType u) {
	int i;
	for (i = 0; i < G.vexnum && G.vexs[i] != u; i++);
	return i;
}

int FirstAdjVex();

// 返回图G中u的第一个邻接节点

1
2
3
4
5
6
7
8
9
int FirstAdjVex(MGraph G, VertexType u) {
	int index = LocateVex(G, u);
	int i;
	for (i = 0; i < G.vexnum; i++) {
		if (G.arcs[index][i].adj != -1) break;
	}
	if (i == G.vexnum) return -1;  // 没有临界点
	else return i;
}

int NextAdjVex();

// 返回G中顶点v相对于u的下一邻接点

1
2
3
4
5
6
7
8
int NextAdjVex(MGraph G, VertexType v, VertexType u) {
	int indexV = LocateVex(G, v);
	int indexU = LocateVex(G, u);
	int index;
	for (index = indexU + 1; index < G.vexnum && G.arcs[indexV][index].adj == -1; index++);
	if (index == G.vexnum) return -1;
	else return index;
}

void showMatrix();

// 打印图的邻接矩阵

1
2
3
4
5
6
void showMatrix(MGraph G) {
	for (int i = 0; i < G.vexnum; i++) {
		for (int j = 0; j < G.vexnum; j++) cout << G.arcs[i][j].adj << " ";
		cout << endl;
	}
}

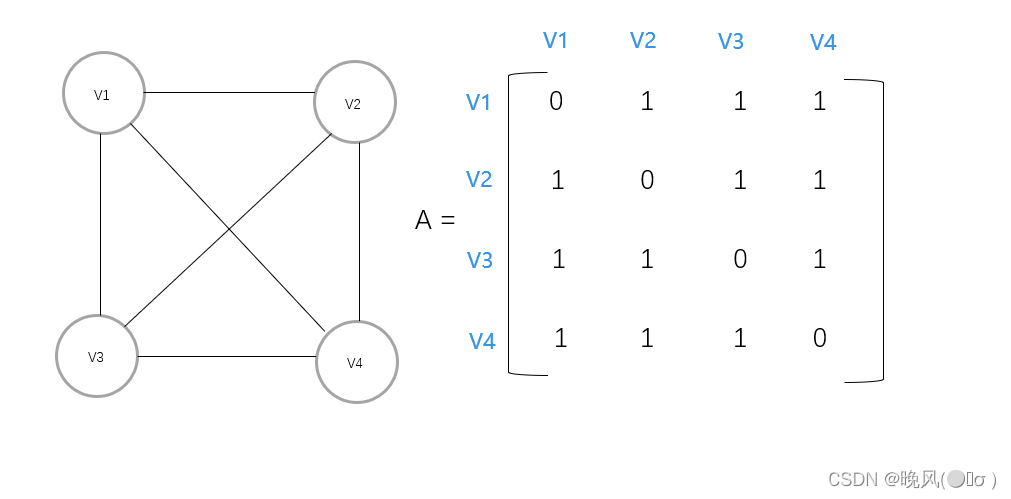
二、图的存储结构

1.邻接矩阵

图没有顺序存储结构，但可以利用二维数组来表示元素之间的关系，即邻接矩阵表示法。

邻接矩阵是表示顶点之间相邻关系的矩阵。

无向图

fd2a45a63a414cfdb6800122ecd6bb82

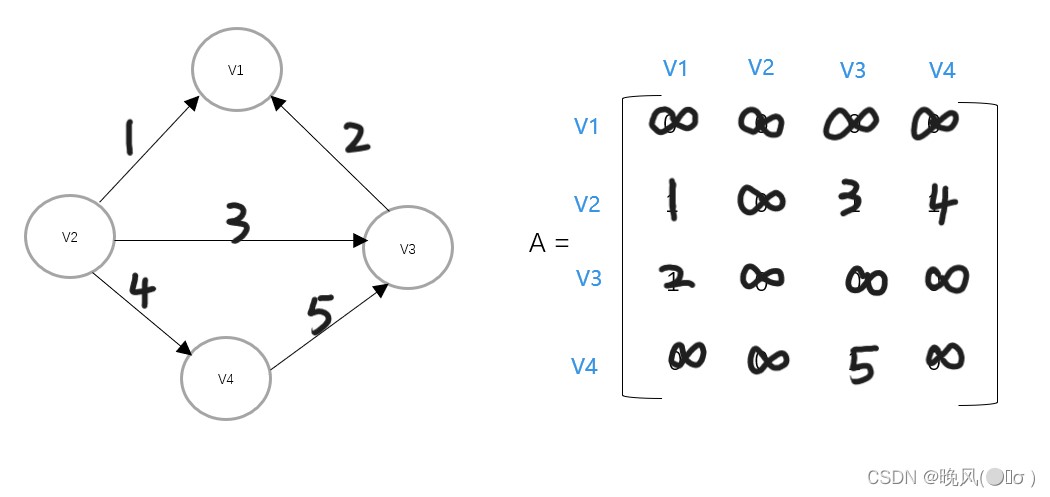
有向网

af06656474c14cfb839a5cb7e8cae998

（1）无向网的定义

1
2
3
4
5
6
7
8
9
10
11
#define MAXINT 32767 //表示极大值，即∞
#define MVnum 100 //最大顶点数

typedef char VerTexType;//假设顶点为字符型
typedef int ArcType; //假设边的权值为整型

typedef struct{
	VerTexType vexs[MVnum]; //顶点表
	ArcType arcs[MVnum][MVnum]; //邻接矩阵
	int vexnum,arcnum; //图的当前点数和边数 
}AMGraph;

（2）无向网的创建

  • 输入总顶点数和总边数；
  • 依次输入点的信息；
  • 初始化邻接矩阵；
  • 依次输入每条边（及其权值），确定两个顶点在图中的位置之后，使相应边赋予相应的权值，同时使其对称边赋予相同的权值。

创建。

无向图的创建只需要删除w变量的部分，并把无穷改成1就好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int CreateUDN(AMGraph &G){ 
	cin>>G.vexnum>>G.arcnum; //输入总点数和总边数
	for(int i=0;i<G.vexnum;i++){
 		cin>>G.vexs[i]; //输入点的信息
	}
	for(int i=0;i<G.arcnum;i++)
	  for(int j=0;i<G.arcnum;j++)
	    G.arcs[i][j]=MAXINT; //初始化邻接矩阵，边的权值均置为∞ 
	for(int k=0;k<G.arcnum;k++) {  // 输入弧v1-v2的信息
		VerTexType v1,v2;int w;
		cin>>v1>>v2>>w; 
		int index1 = LocateVex(G, v1);
		int index2 = LocateVex(G, v2);
		G.arcs[index1][index2]= w; // w表示邻接的权值 
		G.arcs[index2][index1] = G.arcs[index1][index2];  // 无向图对称构造
	}
	return 1;
}

打印。

for(i = 0 ; i < G.vexnum ; ++i){
    for(j = 0; j < G.vexnum; ++j){
        if(j != G.vexnum - 1){
            if(G.arcs[i][j] != MaxInt)
                cout << G.arcs[i][j] << "\t";
            else
                cout << "∞" << "\t";
        }
        else{
            if(G.arcs[i][j] != MaxInt)
                cout << G.arcs[i][j] <<endl;
            else
                cout << "∞" <<endl;
        }
    }
}//for

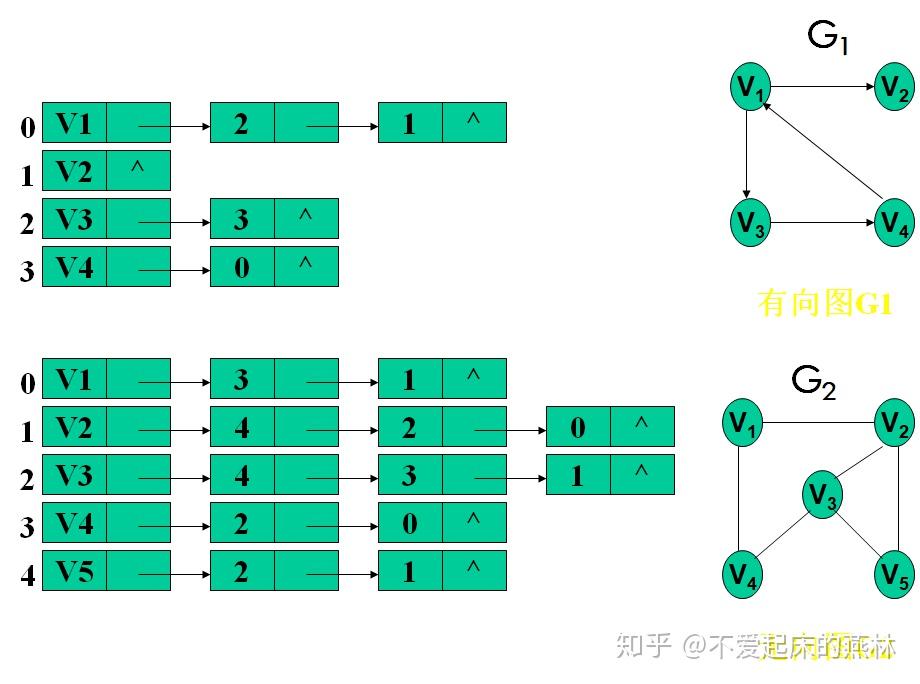
2.邻接表（链式存储）

v2-917733c568ffe18d48b5493b1b327f05_r

（1）定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#typedef MVNum 100 //最大顶点数 
typedef struct ArcNode{ //边结点 
	int adjvex; //该边所指向的顶点的位置
	struct ArcNode *nextarc; //指向下一条边的指针
	//InfoType info         //网的边权值 
}ArcNode;

typedef struct VNode{ //顶点表 
	VertexType data; //顶点信息
	ArcNode *firstarc; //指向第一天依附该结点的弧的指针 
}VNode,AdjList[MVNum];

typedef struct{
	AdjList vertices;
	int vexnum,arcnum; //图的当前顶点数和边数 
}ALGraph;

（2）创建

  • 输入总顶点数和总边数；

  • 依次输入点的信息存在顶点表中，每个表头结点的指针域初始化为NULL；

  • 创建邻接表，依次输入每条边依附的两个顶点，确定这两个顶点的序号i和j之后，将此边结点分别插入vi和vj

  • 对应的两个边链表的头部。如果是有向图，只需生成一个序号为j的边结点，插入到vj的边链表头。

    int CreateUDG(ALGraph &G){
    //采用邻接表表示法，创建无向图G
    cin >> G.vexnum >> G.arcnum; //输入总顶点数，总边数
    for(int i = 0; i < G.vexnum; ++i){ //输入各点，构造表头结点表
    cin >> G.vertices[i].data; //输入顶点值
    G.vertices[i].firstarc=NULL; //初始化表头结点的指针域为NULL
    }//for
    for(int k = 0; k < G.arcnum;++k){ //输入各边，构造邻接表
    VerTexType v1 , v2;
    int i , j;
    cin >> v1 >> v2; //输入一条边依附的两个顶点
    i = LocateVex(G, v1); j = LocateVex(G, v2);
    //确定v1和v2在G中位置，即顶点在G.vertices中的序号

    ArcNode p1=new ArcNode; //生成一个新的边结点p1
    p1->adjvex=j; //邻接点序号为j
    p1->nextarc= G.vertices[i].firstarc; G.vertices[i].firstarc=p1;
    //将新结点p1插入顶点vi的边表头部

    ArcNode p2=new ArcNode; //生成另一个对称的新的边结点p2
    p2->adjvex=i; //邻接点序号为i
    p2->nextarc= G.vertices[j].firstarc; G.vertices[j].firstarc=p2;
    //将新结点    p2插入顶点vj的边表头部
    }//for
    return 1;
    }

三、图的遍历

1.深度优先遍历

设置变量。

图的遍历和树的遍历类似，即从图中某一顶点出发遍历图中其余顶点，且使每一个顶点仅被访问一次。
为了避免同一顶点被访问多次，在遍历图的过程中，必须记下每个已被访问过的顶点。为此，我们可以设一个辅助数组Visited[N]来标记某一顶点是否被访问过了，初始化为False。

1
2
3
bool visited[MVNum];           					//访问标志数组，其初值为"false" 
int FirstAdjVex(Graph G , int v);				//返回v的第一个邻接点
int NextAdjVex(Graph G , int v , int w);		//返回v相对于w的下一个邻接点

类似于树的先序遍历。

  • 从图中某个顶点v出发，访问v，并置visited[v]的值为1；
  • 依次检查v的所有邻接点w，如果visited[w]的值为0，再从w出发进行遍历，直到图中所有顶点都被遍历过。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 图的深度优先遍历
void DFSTraverse(MGraph G) {
	int* visited = new int[G.vexnum]; // 访问标志数组
	for (int i = 0; i < G.vexnum; i++) visited[i] = 0; // 初始化未被访问
	for (int i = 0; i < G.vexnum; i++) {
		if (!visited[i]) DFS(G, i, visited); // 对尚未访问的顶点i调用DFS，
											 // 因为图G可能不是连通图
	}
}
// 从图中第v个顶点开始进行深度优先遍历
void DFS(MGraph G, int v, int* visited) {
	visited[v] = 1; //先访问顶点v
	cout << G.vexs[v] << " ";
	for (int w = FirstAdjVex(G, G.vexs[v]); w >= 0; w = NextAdjVex(G, G.vexs[v], G.vexs[w])) {
		if (!visited[w]) DFS(G, w, visited); // 对v的尚未访问的邻接顶点w递归调用DFS
	}
}

2.广度优先遍历

广度优先搜索（Broadth First Search） 类似于树层次遍历的过程，即以v为初始点，由近即远，一次访问和v有路径相通且路径长度为1，2，…的顶点。此过程可借助于队列实现。

  • 从图中某个顶点出发，访问v，并置visited[v]的值为1，然后v进队；
  • 只要队列不空，则：
  • 队头顶点u出队；
  • 依次检查u的所有邻接点w，如果visited[w]为0，访问w，并置其值为1，w进队。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void BFSTraverse(MGraph G) {
// 按照广度优先非递归遍历图G，使用辅助队列Q和访问标志数组visited。
	int* visited = new int[G.vexnum];
	queue<int> Q;
	int i;
	for (i = 0; i < G.vexnum; i++) visited[i] = 0;
	for (i = 0; i < G.vexnum; i++) {
		if (!visited[i]) { //访问顶点i
			visited[i] = 1;
			cout << G.vexs[i] << " ";
			Q.push(i);
			while (!Q.empty()) {
				int u = Q.front();
				Q.pop(); //取出对头顶点
				for (int w = FirstAdjVex(G, G.vexs[u]); w >= 0; w = NextAdjVex(G, G.vexs[u], G.vexs[w])) {
					if (!visited[w]) {  // w为u的尚未访问的邻接顶点
						visited[w] = 1;
						cout << G.vexs[w] << " ";
						Q.push(w);
					}
				}
			}
		}
	}
}