二叉树的表现

• 一、二叉树的遍历和建立
  • 1.定义
  • 2.建立（按先序遍历的顺序）
  • 3.中序遍历
  • 4.先序遍历
  • 5.后序遍历
  • 6.层序遍历
• 二、复制二叉树
• 三、计算二叉树
  • 1.计算深度
  • 2.计算高度
• 四、计算二叉树的结点数
  • 1.计算结点数
  • 2.计算叶子结点数
• 五、线索二叉树
  • 1.定义
  • 2.创建
  • 3.线索化
  • 4.中序遍历

[TOC]

一、二叉树的遍历和建立

1.定义

（1）顺序存储表示

仅适用于完全二叉树，层序存储

深度k个结点的二叉树（无论完全与否）都需要长度2^k-1的一维数组

#define MAXTSIZE 100
typedef TElemType SqBiTree[MAXTSIZE]; //0号单元存储根结点
SqBiTree bt;

（2）链式存储表示

这里注意data的数据类型是char！不然是返回不了结点的

typedef struct BiTNode{
	char data;
	struct BiTNode *lchild,*rchild; //左右孩子指针 
}BiTNode,*BiTree;

2.建立（按先序遍历的顺序）

• 读入单个字符ch；
• 如果ch是#，看作空树，否则：
• 申请新的结点空间T；
• 把ch赋给T->data；
• 递归创建左、右子树。

void CreateBiTree(BiTree &T){
//按先序遍历的顺序建立二叉链表 
	char ch;
	cin>>ch;
	if(ch == '#') T=NULL; //递归结束
	else{
		T = new BiTNode; //根结点 
		T->data =ch;
		CreateBiTree(T->lchild);//递归创建左子树 
		CreateBiTree(T->rchild);//递归创建右子树 
	} 
}

3.中序遍历

若二叉树为空，则空操作，否则：

• 中序遍历左子树；
• 访问根结点；
• 中序遍历右子树。

（1）递归遍历

void InOrderTraverse(BiTree T){
//中序遍历的递归算法
if(T){
	InOrderTraverse(T->lchild);//中序遍历左子树
	cout<<T->data;
	InOrderTraverse(T->rchild);//中序遍历右子树
} 
}

（2）非递归遍历

①对于STL下的stack容器，如果要使链表结点进出栈，就定义类似于

stack<BiTNode*>stk;

然后就可以照常使用了。

②这一段的工作机制是：

• 从根结点开始，遇到结点则将结点压栈；
• 当遇到无左子树的结点时，将此结点弹栈且访问它并遍历它的右子树；
• 若该结点为叶子结点，则继续弹栈，开始遍历它的父节点的右子树。

③用了一个临时变量BiTNode* top来储存栈顶结点，存完以后stack出栈，top被访问，之后继续遍历

void InOrderTraverse1(BiTree T){
//中序遍历的非递归算法（栈）
stack<BiTNode*>stk; 
BiTNode *p;
p = T;
while (p || !stk.empty()) {    
// 遍历左子树    
if(p) {    
  stk.push(p);    
  p = p->lchild;    
}else{    
  BiTNode* top = stk.top();  // 临时变量存储栈顶元素  
  stk.pop();    
  cout << top->data; // 访问根结点    
  p = top->rchild; // 遍历右子树    
}    
}    

}  

4.先序遍历

（1）递归

若二叉树为空，则空操作，否则：

• 访问根结点；
• 先序遍历左子树；
• 先序遍历右子树。

void PreOrderTraverse(BiTree T){
//先序遍历的递归算法
if(T){
	cout<<T->data;
	PreOrderTraverse(T->lchild);//先序遍历左子树
	PreOrderTraverse(T->rchild);//先序遍历右子树
} 
}

（2）非递归

void PreOrderTraverse1(BiTree T){
//先序遍历的非递归算法（栈）
stack<BiTNode*>stk; 
BiTNode *p;
p = T;
while (p || !stk.empty()) {    
// 遍历左子树    
    if(p) {
	cout<<p->data;   //访问根结点 
    stk.push(p);    //根结点进栈 
    p = p->lchild;   //遍历左子树 
    }else{
	BiTNode* top = stk.top();    
    stk.pop();       
    p = top->rchild; // 遍历右子树    
    }    
    }    
} 

5.后序遍历

（1）递归

若二叉树为空，则空操作，否则：

• 后序遍历左子树；
• 后序遍历右子树。
• 访问根结点；

void PostOrderTraverse(BiTree T){
//后序遍历的递归算法
if(T){
	PostOrderTraverse(T->lchild);//后序遍历左子树
	PostOrderTraverse(T->rchild);//后序遍历右子树
	cout<<T->data;
} 
}

6.层序遍历

（1）队列法

• 将二叉树的根结点进队；
• 判断队不为空，则对根结点进行访问：将队头输出；
• 判断结点有左孩子，就把左孩子进队，结点有右孩子，就把右孩子进队；
• 遍历过的结点出队。

void LevelOrderTraverse(BiTree &T){
//用队列实现层序遍历 
queue<BiTNode*>q;
if(T) q.push(T);//根结点进队
while(!q.empty()){
	cout<<q.front()->data;//访问根结点
	if (q.front()->lchild)   //如果有左孩子，leftChild入队列
    {
        q.push(q.front()->lchild);   
    }
    if (q.front()->rchild)   //如果有右孩子，rightChild入队列
    {
        q.push(q.front()->rchild);
    }
    q.pop();  //已经遍历过的节点出队列
	} 
} 

（2）数组法

• 检查根结点是否为空，如果为空立即返回；
• 创建BiTNode指针类型的指针数组，定义in、out变量，它们模拟了队列的进队和出队，用于跟踪在数组temp中哪个位置是下一个要插入节点的位置（in），以及哪个位置是当前要处理的节点（out）；
• 进队，保存根结点；
• 如果已经进队（in>out)，循环执行以下操作：
• ​ 定义临时结点变量，保存队列头部结点，out出队；
• ​ 如果结点存在，访问结点；
• ​ 检查左、右孩子是否存在，把它们加进队列中。
• 如果in的值溢出，中断返回。

void LevelOrderTraverse1(BiTree T){
//创建结构体数组实现层序遍历
//#define MAXTSIZE 100
if(!T) return;

BiTNode* temp[MAXTSIZE]; ////创建BiTNode指针类型的指针数组
int in=0;
int out=0;
temp[in++]=T;//保存根结点
while(in>out){
	BiTNode* node = temp[out++]; // 取出队列头部节点
	if(node){
	cout<<node->data;//访问结点 
	if (node->lchild) temp[in++] = node->lchild;  
  if (node->rchild) temp[in++] = node->rchild; 
	}
	if(in>MAXTSIZE) return;
}

四种遍历的输出为：

请输入建立二叉链表的序列：
ABC##DE#G##F###
中序遍历的结果为：
CBEGDFA
先序遍历的结果为：
ABCDEGF
后序遍历的结果为：
CGEFDBA
层序遍历的结果为：
ABCDEFG

二、复制二叉树

如果是空树，停止递归，否则：

• 申请一个新结点空间，复制根结点；
• 递归复制左子树、右子树。

void copy(BiTree T,BiTree &NewT){
//复制一颗和T完全相同的二叉树
if(T==NULL){
	NewT=NULL;
	return 0;
}else{
	NewT = new BiTNode;
	NewT->data=T->data;//复制根结点
	copy(T->lchild,NewT->lchild);//递归复制左子树
	copy(T->rchild,NewT->rchild);//递归复制右子树  
}
}

遍历以后可以发现新树和被复制的树完全一致。

三、计算二叉树

1.计算深度

int Depth(BiTree T){
//计算二叉树的深度
int m,n;
if(T==NULL) return 0;
else{
	m=Depth(T->lchild);//递归计算左子树的深度 
	n=Depth(T->rchild);//递归计算右子树的深度
	if(m>n) return m+1;//取更大者 ，+1 是为了加上当前节点这一层
	else return n+1; 
}
}

2.计算高度

int GetHeight( BinTree BT ){
    if(BT == NULL)
        return 0;
    //left
    int left_height = 0, right_height = 0;//定义左子树和右子树的高度变量
    left_height = 1 + GetHeight(BT->Left);//遍历
    //right
    right_height = 1 + GetHeight(BT->Right);//遍历
    if(left_height > right_height)//取更高者
        return left_height;
    else return right_height;
}

四、计算二叉树的结点数

1.计算结点数

int NodeCount(BiTree T) {
	//统计二叉树T中结点的个数
	if (T == NULL) return 0;//如果是空树，则结点个数为0，递归结束
	else return NodeCount(T->lchild) + NodeCount(T->rchild) + 1;
	//否则结点个数为左子树的结点个数+右子树的结点个数+1
}

2.计算叶子结点数

①

void CountLeaf(BiTree T, int& count) //求叶子结点个数 
{
     if(T) {
        if ((!T->lchild)&& (!T->rchild))
           count++;     // 对叶子结点计数	
		CountLeaf( T->lchild, count);  
      	CountLeaf( T->rchild, count); 
   } // if
} // CountLeaf

②

int LeafCount ( BiTree T)
{
    int count=0;

if(T==NULL){//空树
    return 0;
}else if(T->lchild==NULL && T->rchild==NULL){//只有一个根节点
    return count+1;
}else {
    count=LeafCount(T->lchild)+LeafCount(T->rchild);//关系为左右相加求和
    return count;
}

}

五、线索二叉树

解决问题：

• 在n个结点的二叉树中，必定有n+1个空链域（叶子结点的左右子树空间浪费了）
• 二叉树的遍历，无论是递归还是非递归算法，效率都不算高。

线索化：

现将某结点的空指针域指向该结点的前驱后继，定义规则如下

• 若结点的左子树为空，则该结点的左孩子指针指向其前驱结点
• 若结点的右子树为空，则该结点的右孩子指针指向其后继结点

这种指向前驱和后继的指针称为线索，将一棵普通的二叉树以某种次序遍历，并添加线索的过程称为线索化。

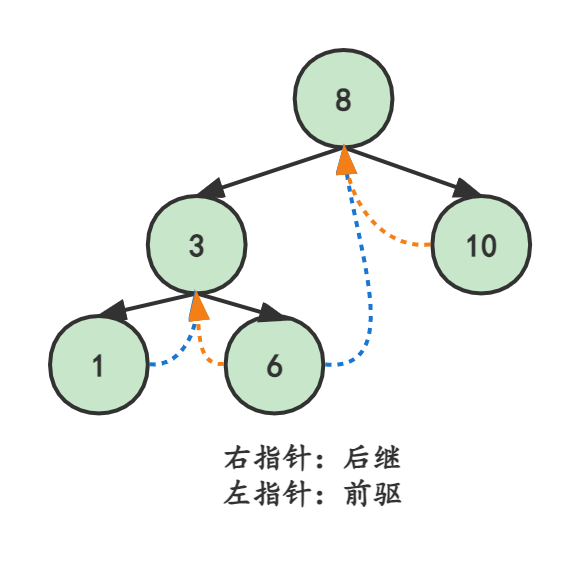
添加标志位ltag和rtag,并定义以下规则

• ltag0，指向左孩子；ltag==1，指向前驱结点
• rtag0，指向右孩子；rtag==1，指向后继结点

从而区分诸如lchild指向的是左孩子还是前驱结点

1.定义

其中pre是全局变量

typedef struct BiThrNode{
	char data;
	struct BiThrNode *lchild,*rchild;
	int Ltag,Rtag;
}BiThrNode,*BiThrTree;


BiThrNode* pre;//前驱结点的变量

2.创建

一定要对Ltag和Rtag初始化！！这里排查了好久

void CreateBiTree(BiThrTree &T){
//按先序遍历的顺序建立二叉链表 
	char ch;
	cin>>ch;
	if(ch == '#') T=NULL; //递归结束
	else{
		T = new BiThrNode; //根结点 
		T->data =ch;
		T->Ltag = 0;       //这里一定要加上，不然后边会出错 
    T->Rtag = 0;
		CreateBiTree(T->lchild);//递归创建左子树 
		CreateBiTree(T->rchild);//递归创建右子树 
	} 
}

3.线索化

• 如果p非空，左子树递归线索化；
• 如果p的左孩子为空，给p加上左线索，Ltag=1，让p的左孩子指针指向pre（前驱）；否则Ltag=0；
• 如果p的右孩子为空，给pre加上右线索，Rtag=1，让pre的右孩子指向p（后继），否则Rtag=0；
• 将pre指向刚访问过的结点p，即pre=p；
• 右子树递归线索化。

void InThreading(BiThrTree p){
	if(p){
    InThreading(p->lchild);   //递归左子树线索化
    if(!p->lchild){           //没有左孩子
        p->Ltag = 1;    //前驱线索
        p->lchild = pre; //左孩子指针指向前驱
    }
    if(!pre->rchild){     //没有右孩子
        pre->Rtag = 1;  //后继线索
        pre->rchild = p; //前驱右孩子指针指向后继(当前结点p)
    }
    pre = p; //保持pre指向p的前驱 
    InThreading(p->rchild);      //递归右子树线索化
    }
}

void InOrderThreading(BiThrTree &Thrt,BiThrTree T){
	Thrt = new BiThrNode;//建立头结点 
	Thrt->Ltag=0;//头结点有左孩子，若树非空，则其左孩子为树根
	Thrt->Rtag=1;//头结点的右孩子指针为右线索
	Thrt->rchild=Thrt;//初始化时右指针指向自己
	if(!T) Thrt->lchild=Thrt;//若树为空，则左指针也指向自己
	else{
		Thrt ->lchild=T;//头结点的左孩子指向根 
		pre = Thrt;//pre初值指向头结点 
		InThreading(T);//对以T为根的二叉树进行线索化
		pre->rchild=Thrt;//结束后，pre为最右结点，pre的右线索指向头结点
		pre->Rtag=1;
		Thrt->rchild=pre;//头结点的右线索指向pre 
	} 
}

4.中序遍历

• 指针p指向根结点；
• p非空或遍历未结束时：
• 沿着左孩子向下，到达最左下结点*p，它是中序的第一个结点；
• 访问*p；
• 沿着右线索反复查找当前结点*p的后继结点并访问后继结点，直至右线索为0或者遍历结束；
• 转向p的右子树。

void InOrderThraverse_Thr(BiThrTree T) {  
    BiThrTree p = T->lchild;  //p指向根结点
    while (p != T) {  //空树或遍历结束时，p==T
    // 遍历左子树  
    while (p->Ltag == 0) p = p->lchild;//沿着左孩子向下
	cout << p->data << " ";   //访问其左子树为空的结点
    while (p->Rtag == 1 && p->rchild != T){  
        p = p->rchild;  
        cout << p->data << " ";  //沿着右线索访问后继结点
    }  
    p = p->rchild;  //转向p的右子树
    }  
}