[TOC]
一、集合的概念和表示
名词解释
集合
把具有共同性质的一些东西汇集成一个整体,就形成一个集合。
元素
汇集成集合的事物叫元素。
描述:元素x属于集合A
记作:x∈A
子集
描述:A集合是B集合的子集
记作:A ⊆ B
真子集
描述 : A集合是B集合的子集 , 并且 A ≠ B,则称A集合是B集合的真子集
记作 : A ⊂ B
真包含关系的性质:
- 反自反性: A ⊄ A
- 反对称性: 如果 A ⊂ B,那么 B ⊄ A
- 传递性: 如果 A ⊂ B, 并且 B ⊂ C, 那么 A ⊂ C
非真子集
描述 : 存在元素x是集合A的元素,不是集合B的元素,并且A、B不相等,则称A集合不是B集合的真子集
记作 : A ⊄ B
空集
描述 : 没有任何元素的集合 , 称为空集合 , 简称为空集
记作 : ∅
- x无解→空集
- 空集是一切集合的子集
- 空集是唯一的
- {∅} ≠ ∅
- 对任何一个集合A,∅ ⊆ A
全集
限定所讨论的集合 , 都是某个集合的子集 , 则称该集合为全集 , 记作 E
幂集
描述 : A集合的全体子集组成的集合称为 A的幂集 ;
记作 : P ( A )
幂集个数定理 : 集合 A中的元素个数∣ A ∣ = n ,则 A的 幂集个数 ∣ P ( A ) ∣ = 2ⁿ
外延性原理
两个集合是相等的,当且仅当它们有相同的成员。(两个集合A和B相等,记作A = B)
集合A和集合B相等的充分必要条件是这两个集合互为子集。
二、集合运算
1.运算

2.性质

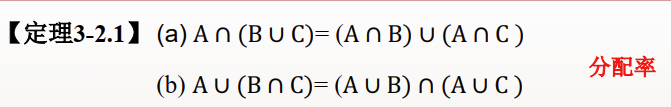
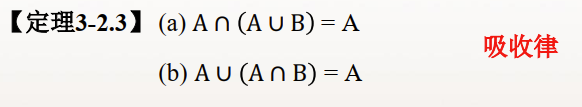

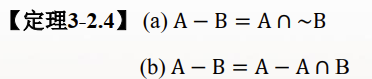
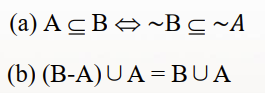


三、包含排斥原理
1.概念




2.例题

四、序偶与笛卡尔积
1.名词解释和原理
序偶
有序二元组的称呼,可以看作一个有顺序的集合,记作<A,B>
序偶不同于集合的是序偶是有顺序的,<A,B> != <B,A>
n元组

笛卡尔积
A与B是集合,那么A与B的笛卡尔积相当于A X B,表示<a,b>,其中:a∈A ,b∈B
笛卡尔积一般不满足交换律和结合律(并、交差运算除外)


2.例题
笛卡尔积的计算

五、关系及其表示
1.名词解释和原理
关系
对于一个二元关系R,R里面的任意一个序偶<x,y>可以记作**<x,y>∈R **或 xRy
A X B的子集R称为一个从A到B的二元关系
前域、值域、域

空关系
A X B的平凡子集∅,称为A到B的空关系。
全域关系
A X B的平凡子集A X B称为A到B的全域关系。
恒等关系
设Iₓ是X上的二元关系,且满足Iₓ = {<x,x>|x∈X},则称Iₓ是X上的恒等关系。
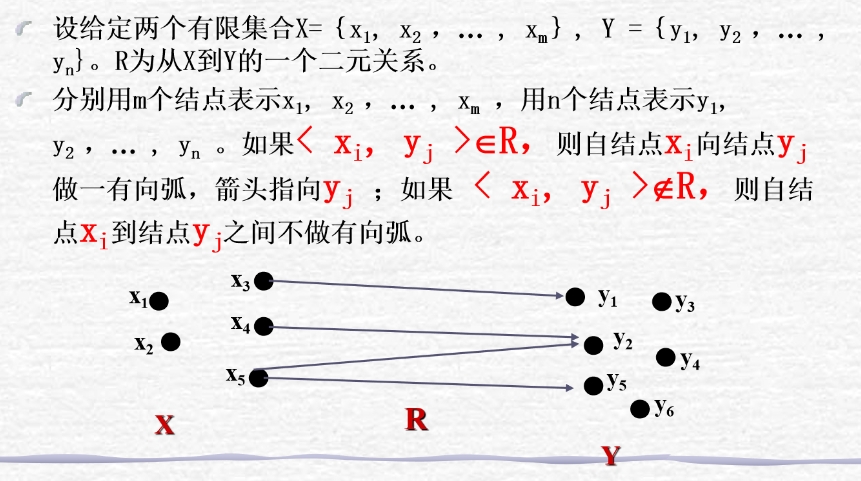
关系矩阵
我们有两个有限集合:X = {x₁,x₂,x₃,……,xₘ},Y={y₁,y₂,y₃,……,yₙ},R是X到Y上的一个二元关系,那么就有相应的关系矩阵:M = [rᵢ ⱼ]ₘₓₙ
rᵢ ⱼ=1当且仅当<aᵢ,bⱼ>∈R
rᵢ ⱼ=0当且仅当<aᵢ,bⱼ>!∈R

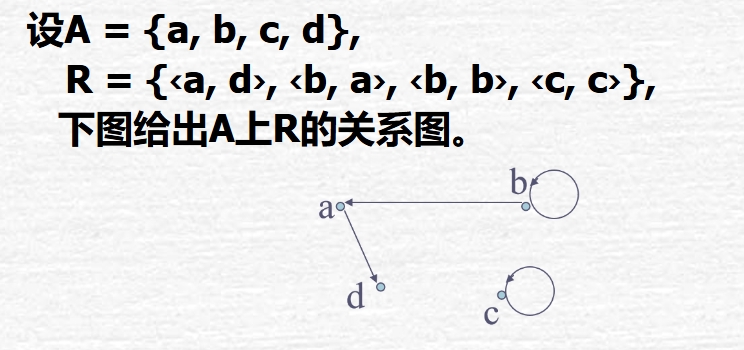
关系图
2.例题
关系矩阵的表示

笛卡尔积的幂集算法

关系图的表示
六、关系的性质
名词解释
自反的关系
R是集合X上面的二元关系,如果对于每一个x ∈A,有xRx,即<x,x>∈R,就称R是自反的。
设集合S非空,S上的关系可以是自反的,是反自反的,也可以两者都不是。
Y是自反的,则:
- Iₓ ⊆ Y;(集合X上的恒等关系是自反关系,但自反关系却不一定是恒等关系)
- Mᵧ主对角线上的元素都是1;
- Gᵧ的每个结点均有环。
反自反关系
R是集合X上面的二元关系,如果对于每一个x ∈A,有xRx,即<x,x>!∈R,就称R是自反的。
Y是反自反的,则:
- Iₓ ∩ Y =∅;
- Mᵧ主对角线上的元素都是0;
- Gᵧ的每个结点均无环。
对称关系
对于关系里面x,y ∈ X,每当xRy,就有yRx,就X上面关系R是对称的。
Y是对称的,则:
- Mᵧ是对称的;
- Gᵧ中任何两个结点之间若有有向边,必有两条方向相反的有向边。
反对称关系
对于关系里面x,y ∈ X,每当xRy和yRx,就有x=y,就X上面关系R是反对称的。
- 关系矩阵以对角线对称的元素不能同时为1,(但可为对称阵,同时为0)。
- 关系图中如果两个结点之间有有向弧,则不能成对出现。
传递关系
对于x, y, z ∈ X,每当xRy, yRz时就有xRz,就称R在X上是传递的。
特殊关系的性质
空关系: 反自反性,对称性,反对称性,传递性
全域关系:自反性,对称性,传递性
恒等关系:自反性,对称性,传递性
总结
- 自反性:应该含有所有<x, x>
对称性:如果有<x, y>就应该有<y, x>
传递性:如果有<x, y>和<y, z>就应该有<x, z> - 反自反性:不应该含有任何<x, x>
反对称性:如果有<x, y>就不应该有<y, x>
例题


七、复合关系和逆关系
1.名词和定理
复合关系
R是X到Y的关系,S是Y到Z的关系,则R和S的复合关系R°S称为R和S的复合关系,表示为:
RoS={<x,z>|x∈X且z∈Z(y∈Y ,<x, y>∈R且<y,z> ∈S)}
复合关系相当于一个个元素进行传递,看是否满足传递关系。
逆关系
R是X到Y的二元关系,把R中每一序偶的元素次序颠倒,得到的关系称为R的逆关系,记作Rᶜ
- xRy == xRᶜy
- 互换R的关系矩阵的行和列,即得Rᶜ的关系矩阵(转置)
- 颠倒R的关系图中每条弧线的箭头方向,即得Rᶜ的关系图
- 空关系的逆是空关系
- R=Rᶜ,则说明R是对称的


复合关系的结合律

复合关系的幂集

复合关系的矩阵表示
(1)布尔加法 == or
(2)布尔乘法 == and
2.例题
复合关系的矩阵表示
