[TOC]
正弦信号
正弦稳态电路:在正弦电源作用下,电路达到稳定工作状态时的正弦稳态电路。
正弦交流信号可以用sin函数表示,也可以用cos函数表示,本书采用sin函数。
1.正弦信号的三要素
一个正弦信号由3个参数确定:最大值、频率(角频率)和初相
(1)正弦交流信号的一般表达式:u(t) = Uₘ sin(ωt + θ)
(2)Uₘ:幅值,表示正弦量所能达到的最大值;又叫峰值或振幅
(3)**(ωt + θ):相位**;θ称为相位角
(4)ω:角频率,是正弦量在单位时间内变化的弧度数,单位rad/s
(5)周期:周期T表示正弦量变化一周需要的时间,单位s
(6)公式:①T=2π/ω
②f=1/T
2.正弦信号的相位差
(1)定义:两个同频率正弦信号在任一时刻的相位之差称为相位差,实际上是初相之差。
(2)符号表示:θ=θᵢ - θᵤ
(3)θ>0,表示i(t)超前于u(t),电流比电压先到达最大值或最小值;
θ<0,表示i(t)滞后于u(t);
θ=0,则称i(t)与u(t)同相,二者同时到达最值;
θ=+-π,则称i(t)与u(t)反相,当i(t)达到最大值时,u(t)达到最小值,反之亦然。
3.正弦信号的有效值
(1)定义:设两个阻值相同的电阻,分别通过周期电流和直流电流,在一个周期内,两个电阻消耗相同的能量,就称该直流电流值为周期电流的有效值。
(2)总结:正弦信号的振幅值等于有效值的√2倍。
Uₘ = √2 U , Iₘ = √2 I
(3)公式表示:i(t)=√2 I sin(ωt + θᵢ)
u(t)=√2 U sin(ωt + θᵤ)
正弦信号的相量表示
1.复数A的表示
(1)代数型、指数型和极型
- 代数型:A=a1 + ja2
- 指数型:A=aeʲᶿ
- 极型:a∠θ
(2)指数型转换为代数型
- 欧拉公式:eʲᶿ = cosθ + jsinθ
- 特别的,e^jπ/2 = cos(π/2) + jsin(π/2) =j
(3)代数型转换为指数型和极型
a = (a₁² + a₂²)^1/2
θ = arctan (a₂/a₁)
常用值:arctan1 = π/4
arctan√3 = π/3
arctan1/√3 = π/6
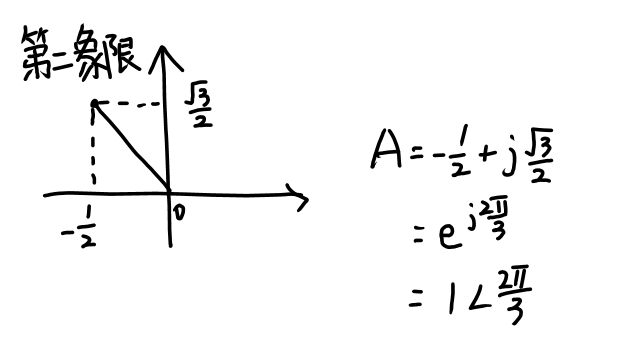
(4)计算
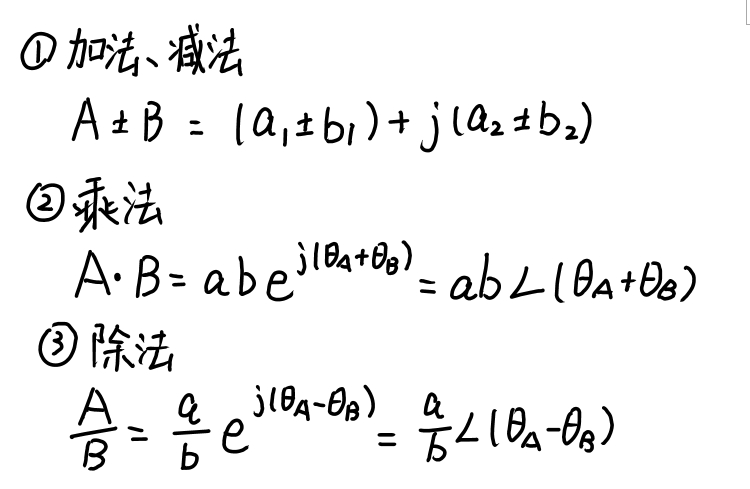
2.用相量表示正弦信号
(1)正弦电流、电压的表示

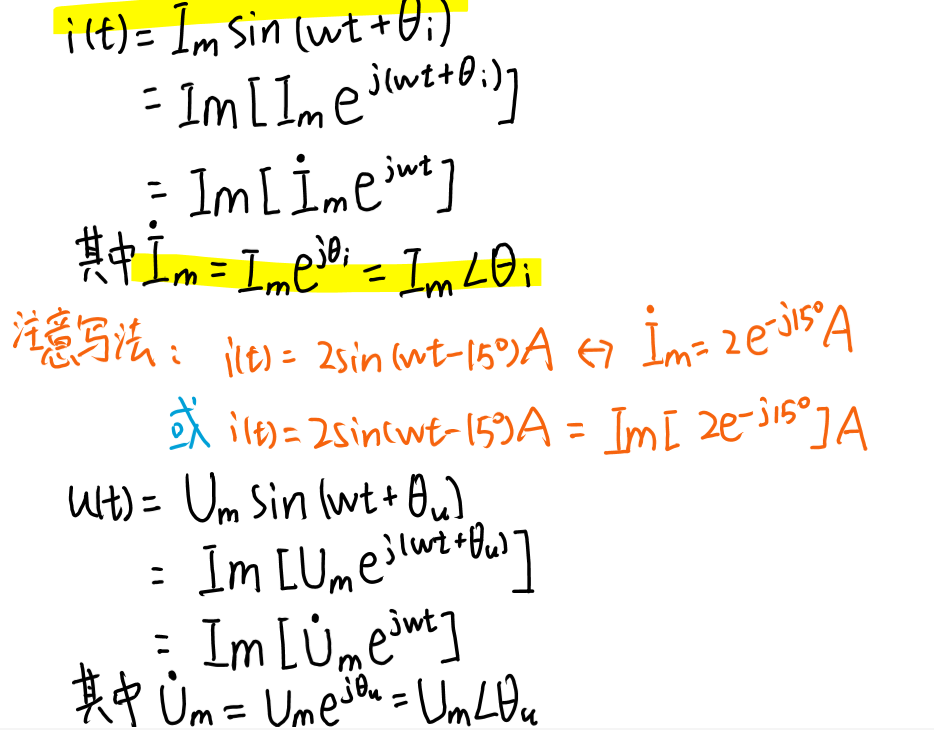
(2)正弦信号与相量的对应规则
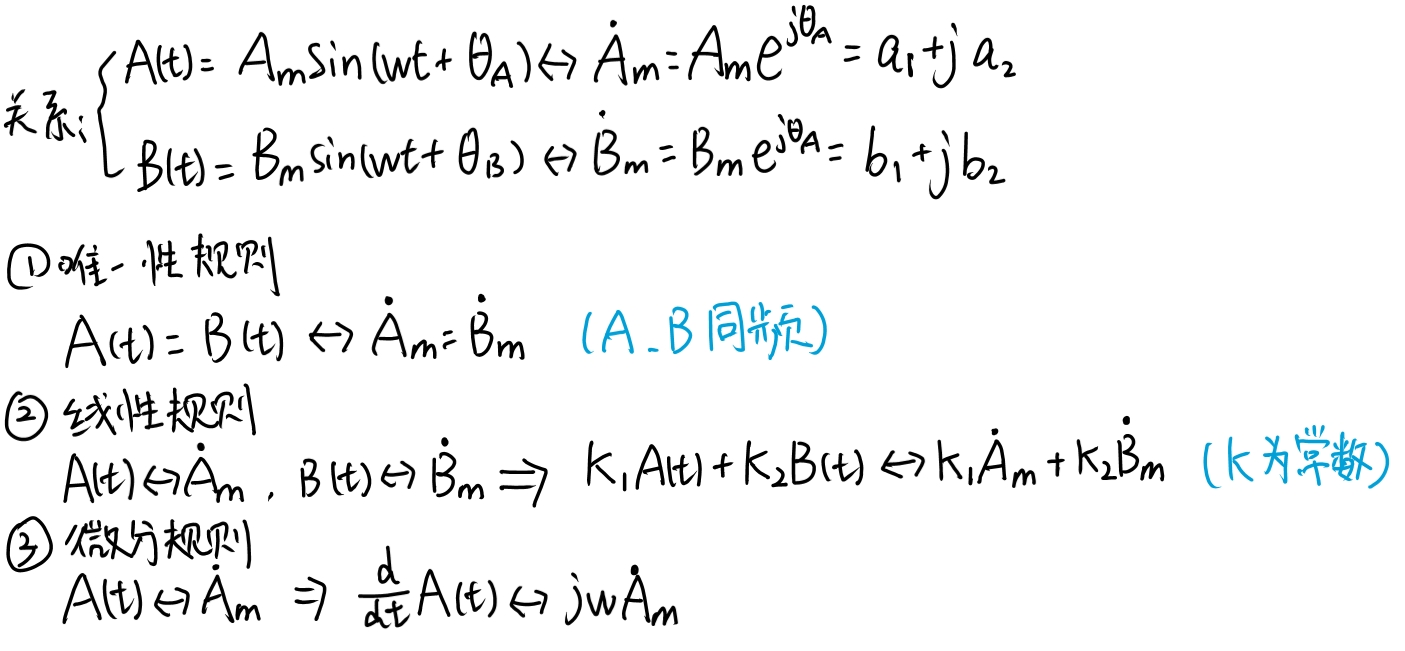
(3)电流相量适用基尔霍夫定律(见例题P87、P91)
由i(t)=i₁(t) + i₂(t),有I˙ =I˙₁ + I˙₂
由u(t)=u₁(t) + u₂(t),有U˙ =U˙₁ + U˙₂
结论对于有效值相量和振幅相量都适用。
基本元件伏安特性的相量形式
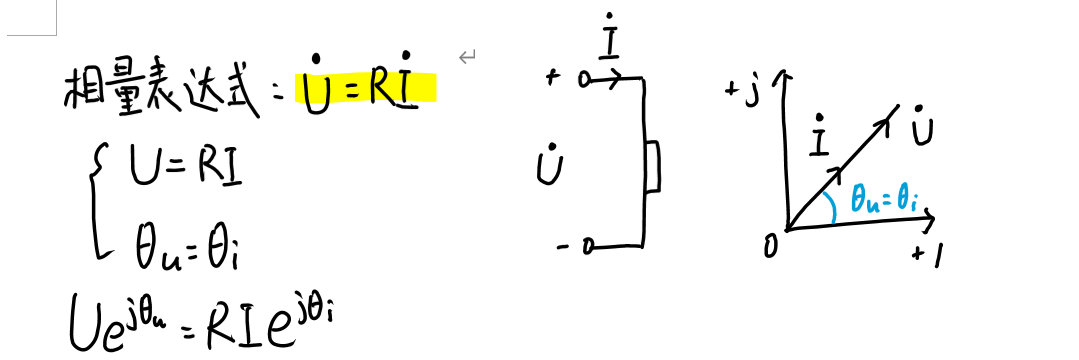
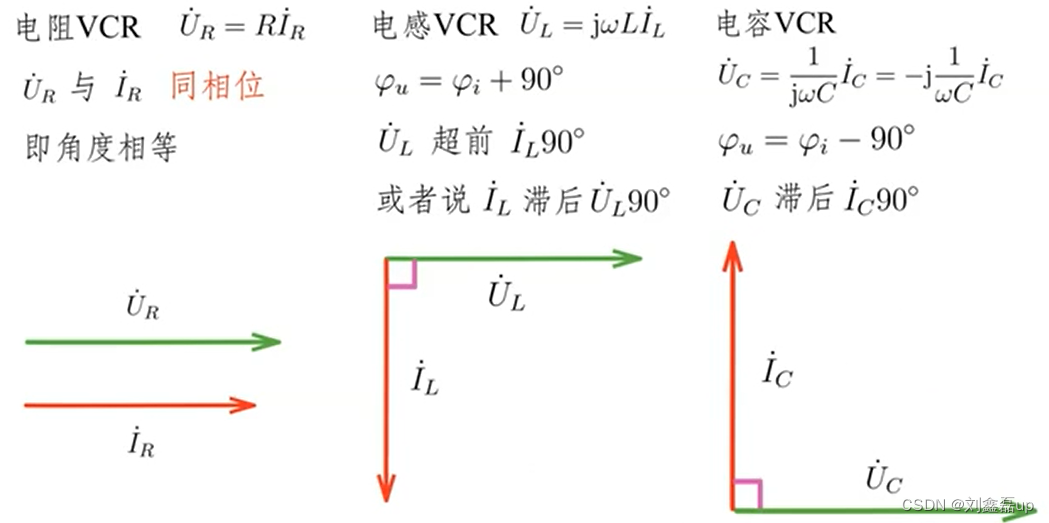
1.电阻元件
2.电感元件
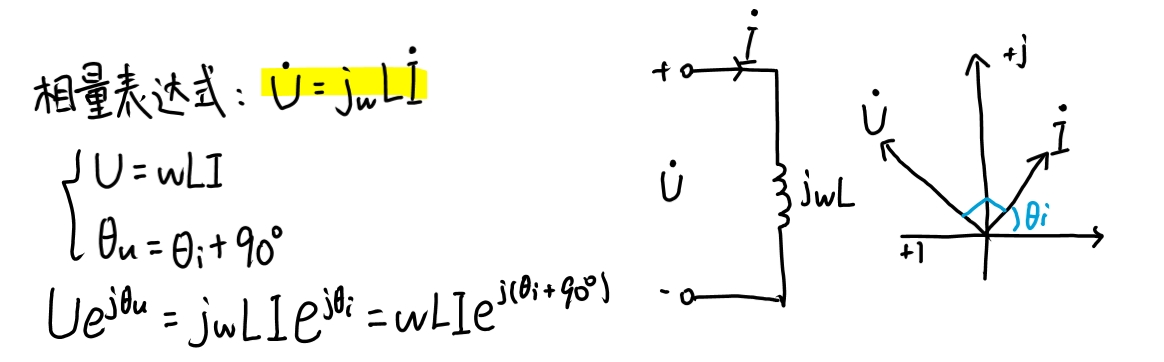
3.电容元件

4.正弦电源的相量模型
①正弦电压源:如果一个独立电压源uₛ(t)的输出电压为正弦电压,即uₛ(t) = √2 Uₛ sin(ωt + θᵤ),就称其为正弦电压源。
参数:Uₛ→有效值;ω→角频率;θᵤ→初相。
②正弦电流源:Iₛ(t) = √2 Iₛ sin(ωt + θᵤ)
③正弦受控源:VCVC,CCVS,VCCS,CCCS
相量模型
1.阻抗和导纳
(1)阻抗Z
①概念
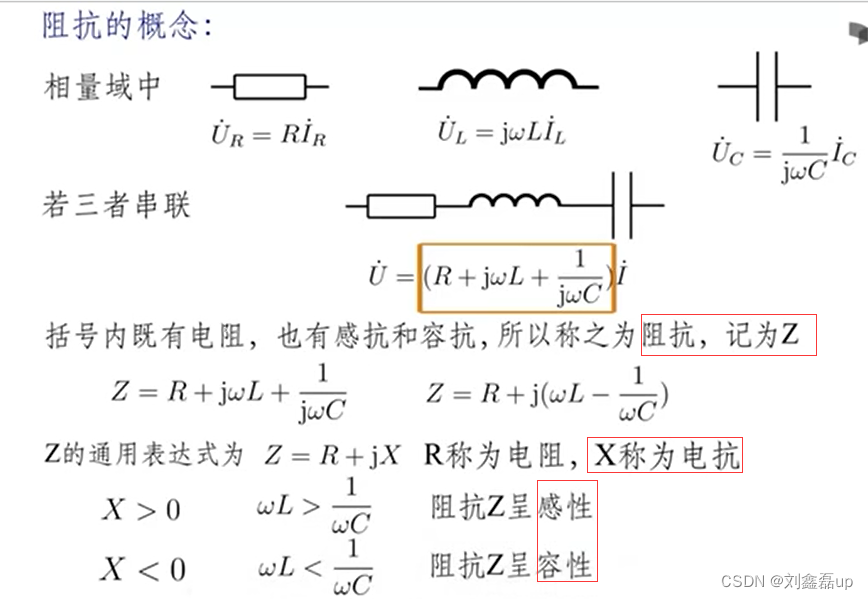
X=0时,阻抗Z成电阻性。
把X替换成φᶻ也成立(z是下标)。
②转换关系
R = |Z|cosφᶻ(z是下标)
X = |Z|sinφᶻ
其中,
|Z| = √(R² + X²) = U/I
φᶻ = arctan(X/R)= θᵤ - θᵢ
③基本元件的阻抗
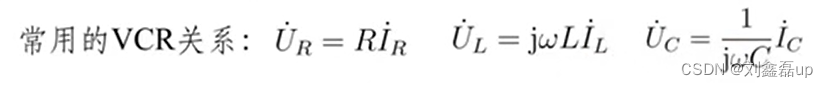
其中,X˪ = ωL,Xᶜ = -1/ωC (c是下标)
(2)导纳Y

导纳的量纲是西门子(S)。
2.相量图
确定相量的角度需要两个步骤:
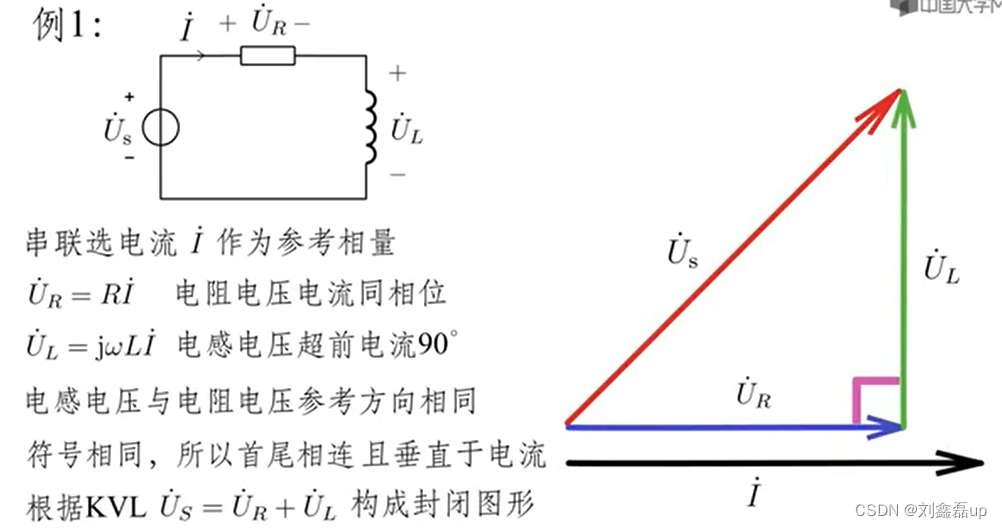
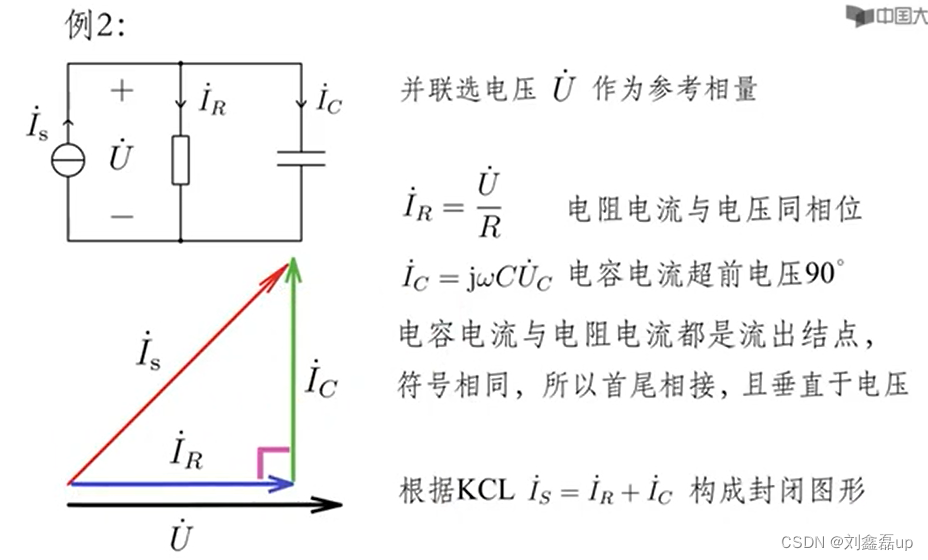
①第1步:确定参考相量,即角度为零的相量
串联电路选电流作为参考相量
并联电路选电压作为参考相量
②第2步:根据支路的VCR确定支路电压或电流相量的角度
滞后:顺时针,后面(以U˪的相量形式作为参照)
超前:逆时针,前面
3.阻抗和导纳的串、并联

串联谐振
1.条件
①电路的总阻抗是:Z = R + j(ωL - 1/ωC)
②发生谐振时,端口电压U`和端口电流I·同相,只有当阻抗的虚部为0才能满足此条件。
③公式:ω = ω₀ = 1 / √(ωC)
2.特征
①谐振时的阻抗最小,电流最大。
②谐振时的电压与电流同相。并且达到最大值。
③谐振时电感电压和电容电压大小相等,方向相反,电阻电压等于电源电压。