[TOC]
8 - 向量代数与空间解析几何
8-1 向量及其线性运算
1.由三角形两边之和大于第三边,有:|a + b|<=|a|+|b|; |a - b|<=|a|+|b|
2.数乘:|λa| = |λ||a|
3.单位向量e=a/|a|
4.a//b等价于b=λa(a!=0)
8-2 空间直角坐标系
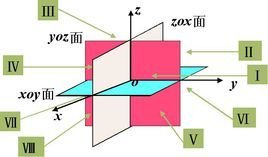
向量OF(x,y,z)是点O关于点F的向径,求点F的坐标就是求向量OP的坐标
①若点F在yoz面上,x=0;
②点F在zox面上,y=0;点F在xoy面上,z=0;
③点F在x轴上,y=z=0;
④点F在y轴上,z=x=0;点F在z轴上,x=y=0;
⑤点F为原点,x=y=z=0。
8-3 向量的综合性质和运算

题型:
1.向量模的坐标表达式
2.两点距离公式:
求证三角形的类型(等腰、直角、等边)
求已知向量的定向单位向量
求与某几点等距离的点
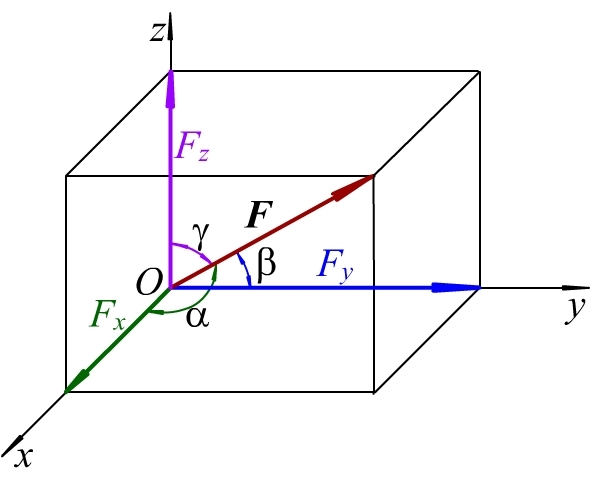
3.方向角与方向余弦:
已知角度求点的坐标
已知向量求方向角、余弦和模
4.投影
已知向量求向量在某轴上的投影
已知投影求向量
8-4 数量积、向量积

题型:
1.用数量积公式求夹角、投影
2.用向量积求三角形面积(用到正弦)
3.用数量积、向量积定义证垂直或平行
4.(多用)用向量积求平面方程
8-5 平面及其方程
1.平面的点法式方程
A(x-x₀)+B(y-y₀)+C(z-z₀)=0
其中n=(A,B,C),M₀=(x₀,y₀,z₀)
2.平面的一般方程
Ax0 + By0 + Cz0 +D=0
n=(A,B,C)
①D=0时,方程表示一个通过原点的平面
②A=0时,n垂直于x轴,方程表示一个平行于(或包含)x轴的平面;B=0,C=0同理
③A=B=0,n同时垂直x轴和y轴,方程表示一个平行于(或重合)x0y面的平面;A=C=0,B=C=0同理
3.平面的截距式方程
x/a + y/b + z/c = 1
a、b、c分别是平面在xyz轴上的截距
4.两平面夹角、点到平面距离
两平面互相垂直相当于A₁A₂ + B₁B₂ + C₁C₂ = 0
两平面互相平行或重合相当于A₁/A₂ = B₁/B₂ = C₁/C₂
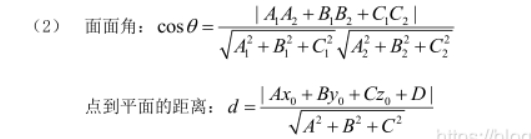
8-6 空间直线及其方程
1.直线的点向式方程(对称式方程)
其中,s=(m,n,p),M₀=(x₀,y₀,z₀)
要素:①方向向量 ②点
2.直线的参数方程
3.直线的一般方程
表现为两个平面的交线
4.线面角
范围是【0,90°】

5.线线角
和面面角公式相同,用cos
6.性质
两直线相互垂直(包括异面、相交)相当于 m₁m₂ + n₁n₂ + p₁p₂ = 0
两直线互相平行或重合 相当于 m₁/m₂ = n₁/n₂ = p₁/p₂
直线与平面平行或直线在平面上 相当于 Am + Bn + Cp =0