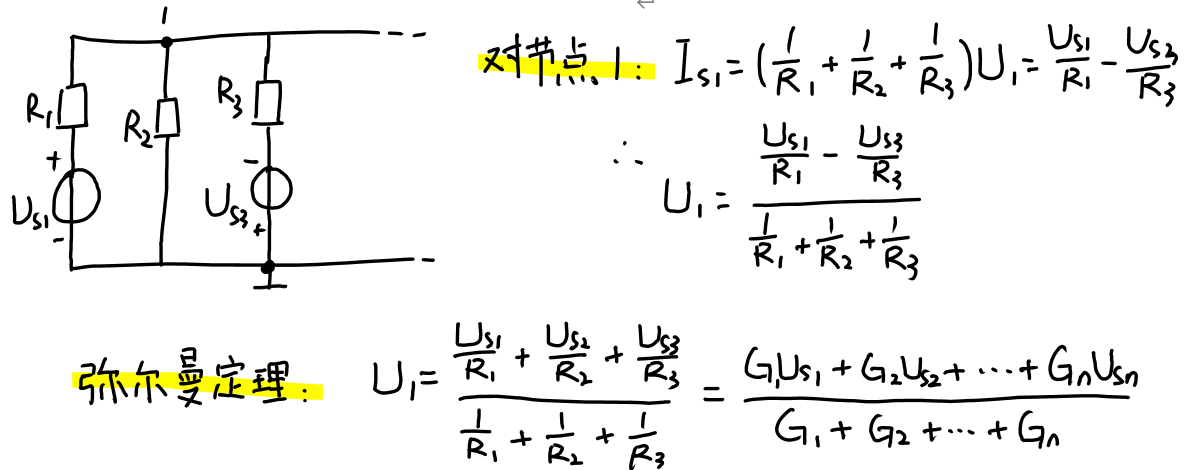[TOC]
电路的基本概念和基本定律
1.电路分析的基本变量
(1)电流
- 电流:是电路中电荷流动量的度量,它代表单位时间流过电路中某一截面的净电荷量。
- 习惯上把正电荷移动的方向规定为电流方向。
- 1A = 10³mA = 10⁶μA
- 恒定电流/直流的大小和方向不随时间变化,用I表示;交变电流/交流用i表示。
- 如果电流的真实方向和参考方向一致,电流为正值。
(2)电压
- 电压:电路中两点之间的电位差。(规定电位下降的方向为电压的真实方向)
- 电位:描述电路中电位能分布的物理量。如果正电荷由a点转移到b点时获得能量,则a点为低电位(负极),b点为高电位(正极)。
- 电压降:电压Uab表示单位正电荷从a点移动到b点所失去的电位能。
- 参考点:又叫“零电位点”,此处的电压为0,用⊥表示。
- 符号:U
- 单位:伏特(V)
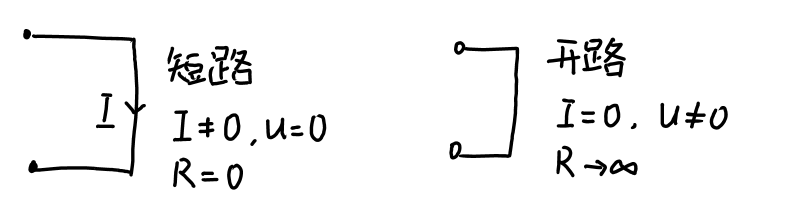
(3)电功率
- 电功率:是电路元件消耗电能快慢的度量,它表示单位时间内电路元件消耗的电场能量。
- 符号:p或p(t)
- 单位:瓦特(W)
- 公式:p= dw/dt = ui; P=UI; (非关联参考方向:p=-ui或P=-UI)
- 功率平衡原理:电路中所有元件的功率之和为0(即能量守恒)。
- 当p>0,p是元件的吸收功率;p<0,元件向外部电路提供功率。
(4)电阻
伏安特性:欧姆定律。
符号:R
单位:欧姆(Ω)
“电阻值”公式:R =U / I(或R=-U/I)
“电阻元件功率”计算公式:PR = U * I = R * i2 = U2 / R
(5)电导
- 符号:G
- 公式:G=1/R,U=1/G,I=GU
- 单位:西门子(S)
- 电阻元件可以用电导来表征。
- G→0,R→∞
2.基尔霍夫定律
(1)术语
- 节点:两条或两条以上的连接点。
- 回路:电路中任一闭合的路径。
- 网孔:回路内部中不含支路的回路。
- 网络:含元件较多的电路。
(2)基尔霍夫电流定律(KCL):
在任意时刻流进任意一个结点的所有支路电流的代数和总是为零。
即:流出=流入。
KCL是运用于电路中节点的,也可以将其推广运用到电路的一个封闭面。
(3)基尔霍夫电压定律(KVL):
在任意时刻绕任意一个回路一周所有支路电压的代数和总是为零。
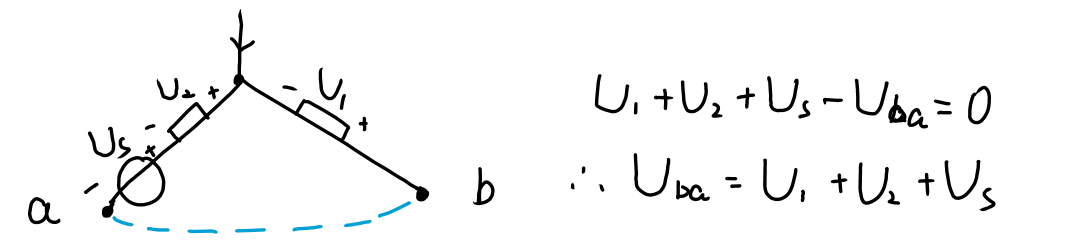
3.电路元件
电路元件是实际电器元件的理想化模型,是构成电路的基本单元。
从元件对能量的表现划分为:耗能元件(电阻元件),供能元件(独立电源),储能元件,能量控制元件。
(1)电阻元件
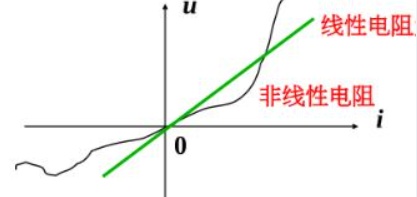
分为线性电阻和非线性电阻。
(2)供能元件
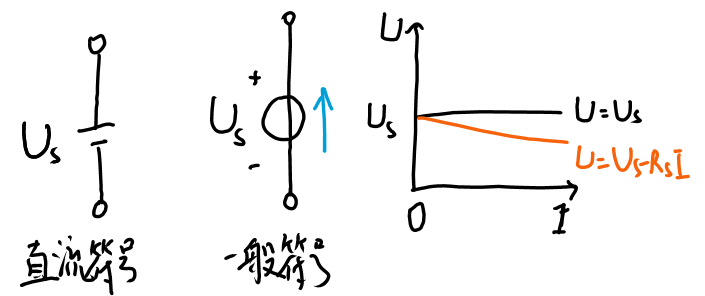
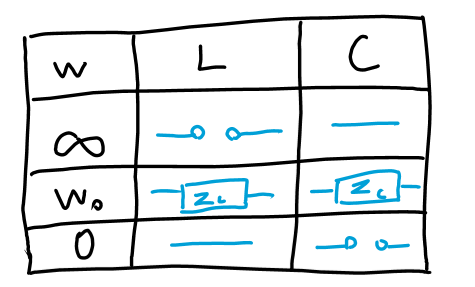
①理想电压源
理想电压源:二端元件两端电压不随流过它的电流变化,保持固定的数值/变化规律。
“理想电压源”的伏安特性: 一条平行于电流轴的直线。
流过理想电压源的电流,是由与之相连接的外部电路来决定的。
②理想电流源
- 理想电流源:二端元件两端电源不随流过它的电压变化,保持固定的数值/变化规律。
- “理想电流源”的伏安特性: 一条平行于电压轴的直线。
- 理想电流源的端电压,是由与之相连接的外部电路决定的。
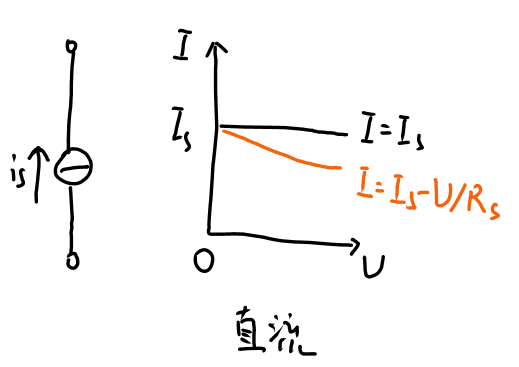
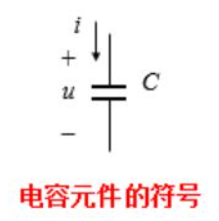
(3)电容元件(例题p19、p20)
- 电容器是一种能储存电场能量的部件。
- 电容元件:指存储在极板上的“电荷量 q ”与两极板之间的“电压 u ”的代数关系。
- 符号:C(电容量)
- 单位:法拉(F)
- 公式:1F = 1C / 1V,**i(t)=Cdu(t)/dt,w=1/2Cu²(t)
- 电容器两端的电压不可能发生跃变(电流→∞)而只能是连续变化的。电容器C在某一时刻的储能只取决于该时刻的电容电压值。
- 两电容器的并联:等效电容量=两电容量之和。C=C1+C2。
相当于电容极板面积增大。
- 两电容器的串联:两电容倒数之和=等效电容量的倒数。1/C=1/C1 + 1/C2 。
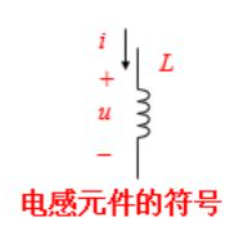
(4)电感元件(例题p23)
- 电感:流过线圈的“磁通量”与流过线圈的“电流 i ”的代数关系。
- 电感元件的原型:空心线圈。
- 符号:L(电感量)
- 单位:亨利(H)
- 公式:**u=L*di/dt(i对t求导),wL=1/2Li²(t)**
- 电感的串联:等效电感量=两电感之和。L=L1+L2。
相当于线圈的匝数增多。
- 电感的并联:两电感倒数之和=等效电感量的倒数。L=1/L1 + 1/L2。
- 电感中电流不能发生跃变。
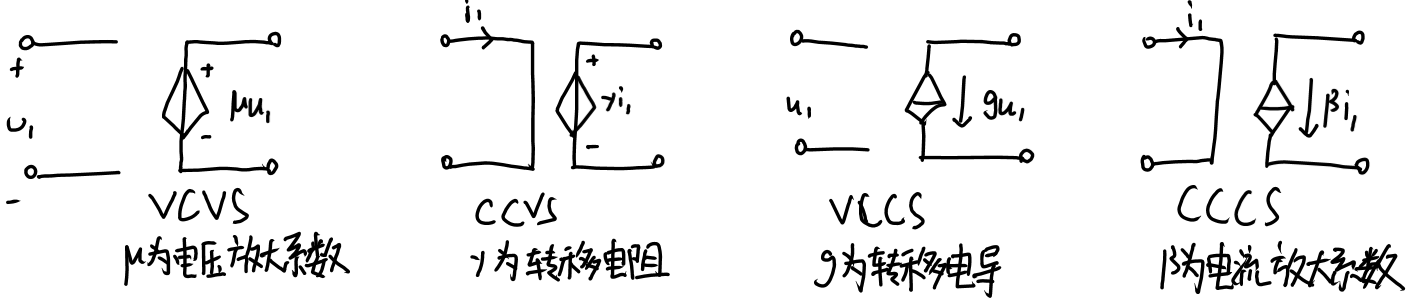
(5)控能元件——受控电源
①VCVS:电压控制电压源
②CCVS:电流控制电压源
③VCCS:电压控制电流源
④CCCS:电流控制电流源
理想:对受控电压源来说,其输出电阻为0;对受控电流源来说,其输出电阻为无限大。对电压控制的受控源来说,其输入电阻为无限大;对电流控制的受控源来说,其输入电阻为0。
在电路分析时,受控源可看作独立电源,然后进行电源的等效变换。
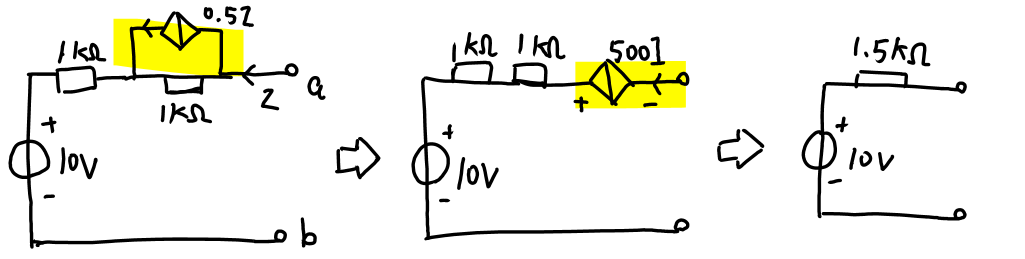
电阻电路的一般分析方法
等效电路分析法
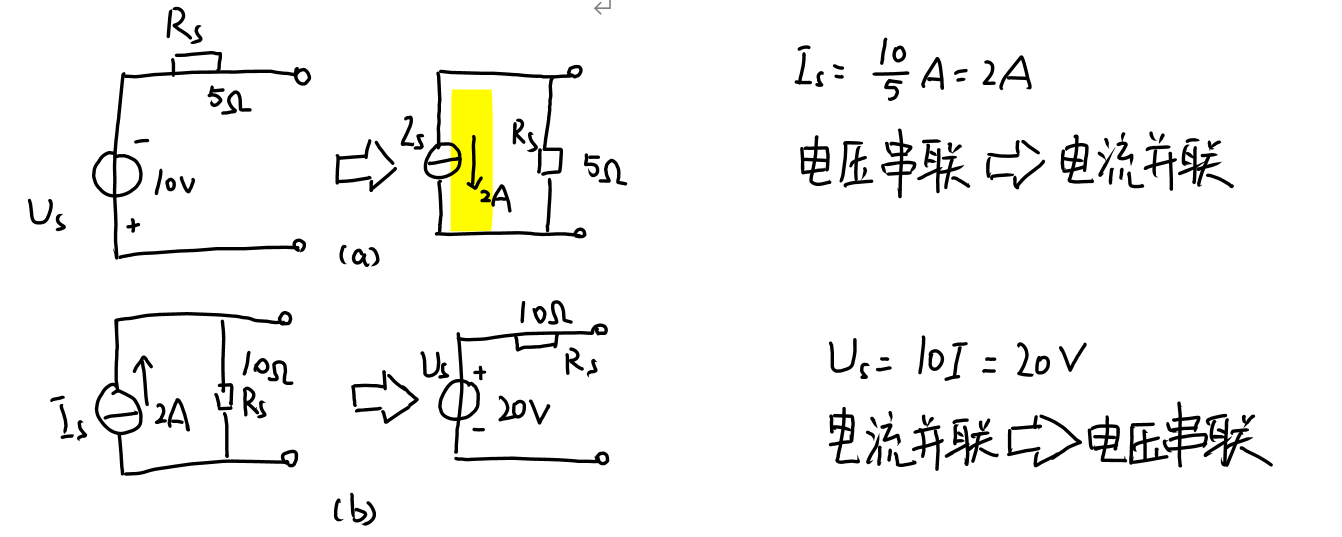
1.电源模型的等效互换
电源等效互换的依据是电源的外特性相同。
(1)等效电路:两个电路具有完全相同的“对外连接端”,两者分别和任意其他的电路成分构成完整电路,如果电路的其它部分工作完全一致,则这两个电路互为等效电路。
(2)电路外特性:电路外接端上的电压与电流之间的关系。每个元件可视为一个电路部分,它的特性即是外特性。
电路中的一部分用其等效电路替换后,电路其它部分的工作情况保持不变;等效只能适合用于外部,对于互相等效的两个电路内部工作一般是不等效的。
2.电阻的串联和并联
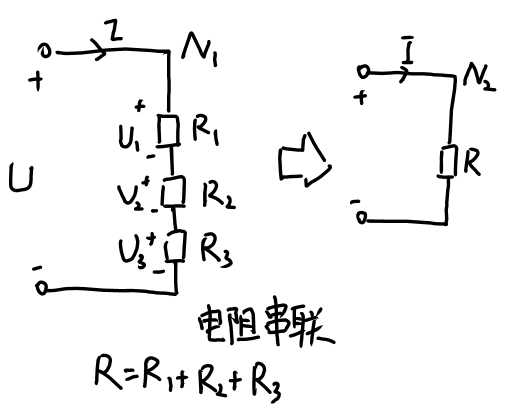
(1)串联
- “电阻串联”等效为“单个电阻元件”;
- 两个电阻串联的等效条件:R = R1 + R2;
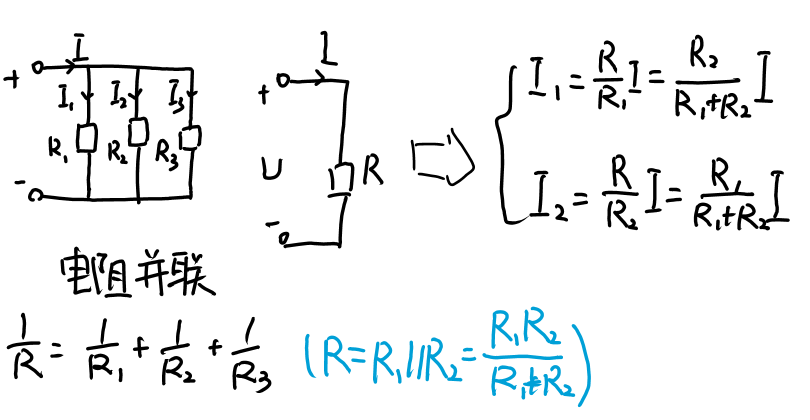
(2)并联
- “电阻并联”也等效为“单个电阻元件”;
- 两个电阻并联的等效条件: G = G1 + G2 或 R = R1 * R2 / R1 + R2
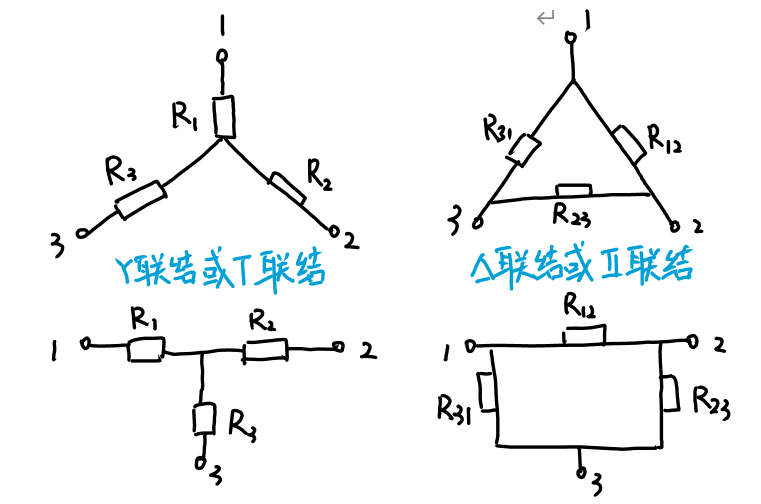
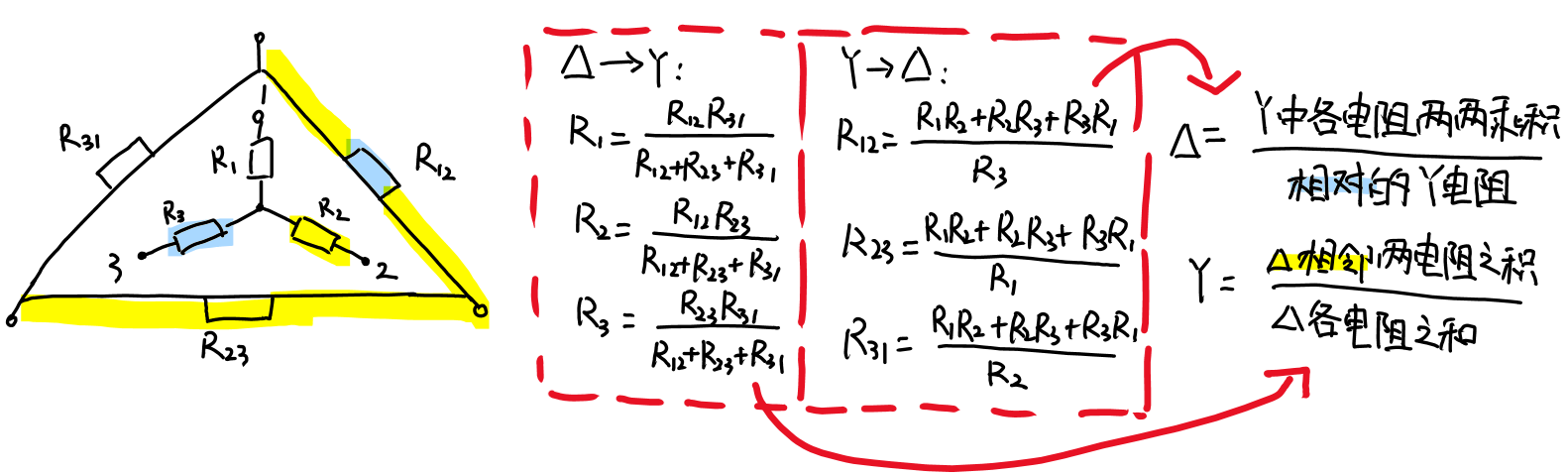
3.电阻的混联及Y-Δ等效变换
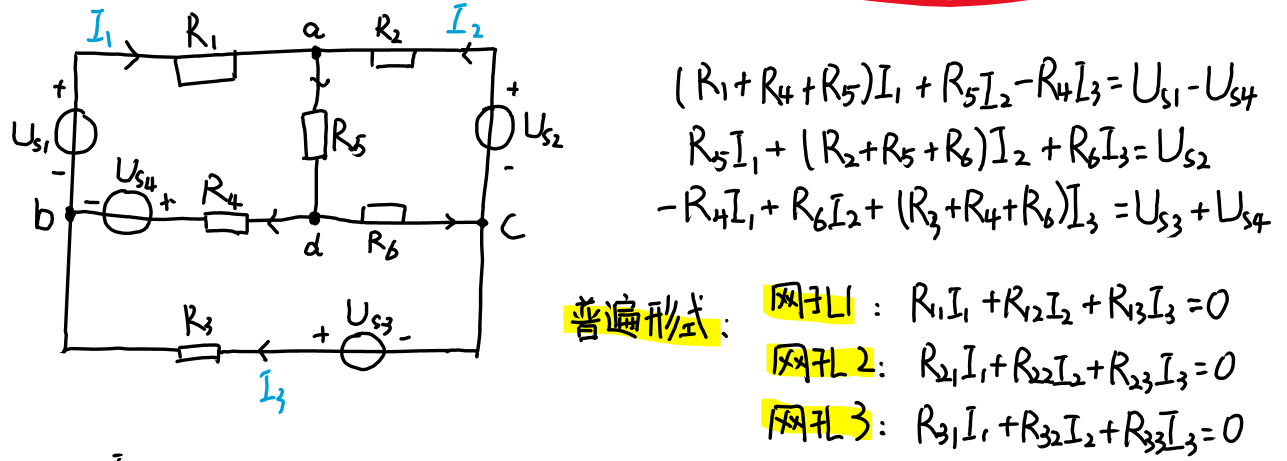
网孔分析法(例题p39)
- 对支路电流法所列的方程中做如下处理,可得到网孔方程:
1)对每个网孔按顺时针方向设定一个网孔电流;
2)将各支路电流表示成网孔电流的叠加。 - 将含源支路转化为电压源U与电阻R串联的形式。
- 自电阻总是正的,而互电阻既可为正也可为负,取决于流过互电阻的两个网孔电流是否一致,一致时取正。
节点分析法
- 选取参考节点如4,则节点4的电位为0,其他3个节点分别对参考节点的电位是U1,U2,U3,即为节点电位。
- 将含源支路转化为电流源I与电导G并联的形式。

总结:①网络的独立节点数少于网孔数,用节点分析法。
②已知的电源是电流源,用节点分析法;电源是电压源,用网孔分析法。
③网孔分析法只适合平面网络。
弥尔曼定理